Revolution Proof of Stake — DeSo (The Decentralized Social Layer-1 Blockchain)

Revolution Proof of Stake

Proof of Stake — Without the Centralization • April 4, 2023

Authors: Nader Al-Naji, Isaac Anthony, Sofonias Assefa, Jackson Dean, Jason Mazursky, Piotr Nojszewski, Jonathan Pollock, Steven Zeller

Abstract

Revolution aims to be the first Proof of Stake protocol that is truly decentralized, censorship-resistant, permissionless, and easy-to-understand. In keeping with this, we strive to make this document comprehensive and straightforward to the point where anyone with basic Computer Science knowledge can read, understand, and implement the entire system from scratch.

Revolution enhances decentralization, censorship-resistance, and protocol complexity compared to earlier Proof of Stake schemes employed by Ethereum, Cosmos, Flow, and Solana. Compared to Proof of Work schemes like Bitcoin, Revolution offers better censorship-resistance due its introduction of the Revolution Rule concept, and maintains the same level of decentralization and protocol complexity without the need for wasteful computation, and without making any significant trade-offs.

Introduction

In this document, we present Revolution Proof of Stake (PoS), a new state-of-the-art Proof of Stake system designed to:

Eliminate centralization risks associated with other PoS protocols, especially those caused by liquid staking on protocols like Ethereum and Cosmos. This is achieved by two novel mechanisms we introduce called Sovereign Staking and Liquid Bonding. Our goal is for Revolution to finally make Proof of Stake systems as decentralized as Proof of Work systems like Bitcoin.
Eliminate censorship risks, making it so that a high-fee transaction is guaranteed to be included in a block within a few seconds of being submitted to the network under normal conditions. This is achieved by two new concepts we introduce called The Revolution Rule, from which the Revolution protocol derives its name, and a novel approach to leader scheduling we call Line of Succession Leader Scheduling.
Eliminate miner-extractable value issues (MEV), making it impossible for block producers to exploit users of the protocol. This is a second benefit of The Revolution Rule concept we introduce.
Scale to tens of thousands of nodes, without incurring quadratic communication overhead like other PoS schemes, including Ethereum. This is possible thanks to Revolution introducing the first production implementation of the Fast HotStuff consensus algorithm.
Remain fully permissionless, allowing anyone to join the network and produce blocks, just like Bitcoin. This is possible thanks to a combination of a novel randomness scheme we call Collaborand, as well as a novel bootstrapping scheme we call HyperSync Bootstrapping.
Eliminate developer oligarchy by introducing a novel and decentralized means of updating protocol-level parameters that we call On-Chain Amendments.
Maximize deflation by introducing a burn-maximizing fee algorithm that improves significantly on Ethereum's state-of-the-art EIP-1159. We call this fee algorithm The BMF, short for "burn-maximizing fees."
Minimize the cost of running a node by introducing a novel Dynamic Block Reward concept that adjusts the block reward to maximize both the amount staked as well as the number of validators, at minimum cost to the protocol.
Maximize simplicity of the protocol, making it understandable by anyone with basic knowledge of Computer Science, similar to Bitcoin's Proof of Work. Where other PoS schemes are riddled with convoluted jargon, making them difficult to follow and verify, Revolution prioritizes simplicity at the protocol level.
- We believe this is the most important thing that Bitcoin got right, with its simplicity allowing the mind-virus to spread, and we hope to bring that same simplicity and ease-of-understanding to Proof of Stake systems with Revolution.
Reduce finality time compared to state-of-the-art Proof of Stake systems, including Ethereum, Cosmos, Solana and Flow.

In order to achieve all of the above goals, Revolution introduces several innovations that we discuss in detail. Below is a summary of all of Revolution's more interesting contributions to the field:

Sovereign Staking (aka No-Lockup Staking). Most existing PoS mechanisms force users to lock up coins for long periods of time, often years, in order to stake. This not only causes centralization on "liquid staking" pools like Lido, but it also causes the protocol to be capital-inefficient in the sense that it now needs to pay validators much more via inflation to support the security of the network. In contrast, Revolution provides the same level of security as "long-lockup" mechanisms, but it only requires locking stake for roughly three hours (three Revolution epochs).
- Aside from significantly improving security and significantly reducing the amount that needs to be paid to validators as inflation, Sovereign Staking also reduces the regulatory risk associated with a protocol's token. This is because validators are paid solely for their work of validating blocks, rather than as a return on amount staked.
Production Fast-Hotstuff. The first production implementation of the Fast Hotstuff consensus algorithm. This allows Revolution to achieve the theoretically-optimal number of rounds of communication per block finalization, with a protocol that is both easy to understand and easy to debug.
Line of Succession Leader Scheduling. A novel leader selection scheme that significantly improves throughput and transaction finality time, without compromising on decentralization or censorship-resistance. This is achieved by allowing a single leader to remain the block producer until either their term expires (~1 hour) or they are caught provably censoring transactions.
The Revolution Rule. A novel mechanism that, when combined with Fast Hotstuff and Line of Succession Leader Scheduling, allows nodes to automatically timeout leaders that they believe to be censoring mempool transactions or extracting MEV. The end result is that transactions cannot be censored for more than a few seconds at most, even when leaders are acting maliciously.
Collaborand. A novel scheme for generating robust on-chain randomness, that innovates materially on all prior schemes. This is needed for any Proof of Stake consensus mechanism to function efficiently.
Elliptic Sum. A novel scheme for verifying that two nodes have the exact same state, without needing to store, index, and update a Mmerkle tree of every account. This cuts state storage costs in half, and increases the efficiency of modifying node state by an order of magnitude over previous state-of-the-art schemes.
Hypersync Bootstrapping. A permissionless way for a new node to join the network and efficiently download a potentially-sharded copy of the state, while being confident that its end-state is consistent with a majority of its peers.
On-Chain Amendments. A novel way of updating key PoS parameters via direct and safe on-chain voting. Whereas other protocols have "secret knobs" that an oligarchy of developers are in charge of updating behind the scenes, Revolution's introduction of on-chain amendments makes it so that all of Revolution's key parameters, including critical economic parameters like block rewards and yields, can now be modified with full transparency, and with full consent of the governed (namely the token-holders).
- This aspect of Revolution truly embodies the principle of "by the token-holders, for the token-holders," ensuring that the protocol maximally serves the interests of token-holders in the long run. This is more important than it seems because critical economic parameters like block rewards and yields will ultimately reflect the interests of token-holders rather than the interests of an oligarchy of developers.
The Burn-Maximizing Fee Algorithm (the BMF). A novel way of computing validator transaction fees that improves significantly on EIP1159, which is widely considered to be the state of the art. The BMF improves on EIP1159 especially during times of high-congestion, which is when fees are most lucrative to the protocol.
The Dynamic Block Reward (the DBR). A novel way of automatically adjusting validator block rewards to explicitly incentivize the total amount staked and the total number of validators on the network. Whereas other schemes dramatically over-pay validators for their services, the DBR ensures that validators are paid no more than their operating costs in the steady-state.
- Sovereign staking, the BMF, and the DBR all combine to create a far more deflationary protocol than has ever existed in the past. In particular, while sovereign staking and the DBR reduce emissions to the absolute minimum, the BMF maximizes the amount burned from transaction fees on the other side, thus making Revolution's deflation rate as close to optimum as possible.
Magic Nonces. A novel scheme for preventing transaction replay attacks that allows transactions to be re-ordered without needing to store a hash of every transaction that has ever been submitted to the network. Improves significantly on Ethereum's consecutive nonce scheme.
NetBoot. A novel way for a new node that joins the network to learn about all of its potential peers that is significantly more decentralized and more censorship-resistant than state-of-the-art DNS Bootstrapping employed by Bitcoin and Ethereum.
Liquid Bonding. (e.g. treasury.deso.com). Although Sovereign Staking means that nobody needs to lock up stake in order to secure the network, it is important to note that incentivizing people to lock up stake could be valuable for other reasons. As such, Revolution leaves blockchains the full freedom to design their lockup schemes however they want. This is achieved by introducing a separate and distinct YieldLock transaction type, which allows users to convert coins into bonds that earn a yield at a set maturity date.
- Importantly, Liquid Bonding allows users to lock up coins and earn a yield without introducing the centralization risks associated with liquid-staking providers like Lido. This is because users who decide to lock coins receive a liquid asset called a bond that is fungible with other bonds with the same maturity, but distinct from the protocol's main coin.
The separation of yield from protocol-level security allows node operators to collectively create arbitrarily-complex yield ladders that are not only much better at fulfilling the needs of the protocol, but that also fully separate any regulatory concerns from the security of the network. Also note that adding Liquid Bonding to a protocol is strictly optional in the sense that the network would be completely secure without it.

In what follows, we describe the Revolution PoS scheme in full detail while providing enough background that an audience that is only somewhat familiar with existing PoS schemes can understand it. For readers who are highly-literate and up-to-date on existing PoS schemes, the background section can be skipped.

Background on Proof of Stake Mechanisms

In this section, we do our best to get the reader up to speed on the existing state of the art when it comes to Proof of Stake. If the reader is already familiar with Proof of Stake schemes, such as Tendermint and HotStuff, this whole section can be skipped.

Starting with Proof of Work

To understand Proof of Stake, it is useful to understand the Proof of Work (PoW) consensus mechanism used by Bitcoin, and then work our way up from there.

When a user initiates a transaction on a Proof of Work blockchain like Bitcoin, it is broadcast to the network and added to a pool of unconfirmed transactions, often referred to as the mempool. Miners on the network then compete to validate and confirm these transactions by solving a complex mathematical puzzle through the proof of work algorithm.

Once a miner successfully solves the puzzle, they add a new block of transactions to the blockchain and broadcast it to the network. This new block contains a cryptographic hash of the previous block, which ensures that the blocks are linked together in a chain and cannot be tampered with or altered without effectively redoing all of the previous work that was done to solve the previous mathematical puzzles in the chain.

As more blocks are added to the chain, it becomes increasingly difficult to change any of the previous transactions, as doing so would require a significant amount of computational power to recalculate all the subsequent blocks in the chain. This creates a high degree of security and trust in the network, as transactions that have been confirmed by a sufficient number of blocks, usually taken to be six blocks for Bitcoin, are considered final and irreversible.

From Proof of Work to Proof of Stake (Tendermint)

At a high level, PoW chains can be considered to be holding an implicit vote among all of the miners on the network for each bundle of transactions, whereby each miner's vote is weighted by how much computational power they have. Each block, a delegate is selected to propose a block, where their likelihood of being selected is weighted by their mining power. In proposing a block, the miner not only casts their vote for the new bundle of transactions they're submitting to their peers, but they also cast their vote for all previous transactions in the chain submitted by other miners. As such, after enough blocks have mined on top of your transaction, you can be confident that a significant majority of the mining power has agreed to include it, thus finalizing it.

Proof of Stake schemes refer to their consensus nodes as validators rather than miners, and they generally consider the weight of a validator's voting power to be proportional to the number of coins staked, or delegated, to them rather than the amount of mining power they have. Additionally, most PoS schemes refer to block production in terms of views or slots. This is where the similarities between PoW schemes and PoS schemes start to diverge.

Unlike PoW schemes, PoS schemes attempt to finalize transactions by an explicit stake-weighted vote on each block via what's known as a two-phase commit scheme. The reason why this two-phase scheme works is complex, and discussed in full detail in Tendermint's paper here. However, it is lucky that the actual mechanism itself is relatively easy to explain at a high level, even though the proof is fairly involved. We explain a basic version of this two-phase commit scheme below, along with an intuitive explanation for why it works:

First, a leader is selected via a stake-weighted random sample of all validators. This leader bundles transactions into a block and sends this block to all other validators. This is often referred to as a pre-prepare message.
- Note that how the leader is selected is an important detail that differs significantly from Proof of Work. Whereas PoW leaders are selected based on their ability to find a winning block hash, PoS leaders are selected deterministically using some source of on-chain randomness. For now, all you need to know is that all validators know and agree on who will be the leader for view N.
After receiving a block, each validator first lets everyone know that they've seen the block and think it's valid by broadcasting a prepare message to all other validators.
- The messages between validators are often referred to simply as votes, as we will discuss later on.
In a second phase, each validator lets everyone know that they've seen that everyone has seen this block. This is done by broadcasting a commit message to all other validators only after they have seen a prepare message come in from a 2/3rds majority of all validators, weighted by stake.
- As an example, if there are five validators, and each validator has 100 coins staked to them, then a 2/3rds stake-weighted majority would be reached after receiving a prepare message from validators representing at least 2/3 * 500 total coins = ~333 coins, or four out of the five validators (representing 400 out of 500 coins, or a 4/5ths majority).
- The reason why a 2/3rds majority is used as the threshold for entering the second phase here is discussed in detail in Tendermint's proofs here. But again, it's OK to take it as a given for the purpose of understanding how the mechanism works.
- Put simply, once a validator has received a prepare message from a 2/3rds majority of all validators, they become confident that this 2/3rds majority has both seen the block and thinks it's valid.
Once a validator has received a commit message from 2/3rds of all validators, weighted by stake, they finalize the block, making it so that no message from any other validator will ever revert the block or the transactions within it.
Conceptually, a block is finalized when you are confident that everyone has both seen the block and confident that everyone has seen that everyone else has seen the block.
It is sufficient to understand that considering a block as finalized after you've seen that everyone else has seen it is safe in the sense that no two validators will ever commit conflicting blocks, and the block will never be reverted as long as 2/3rds of the validators, weighted by stake, are behaving honestly.

The above scheme is often referred to as a PBFT scheme, short for practical byzantine fault-tolerant, and it was refined in the Tendermint consensus protocol utilized by the Cosmos blockchain (here, byzantine can generally be considered synonymous with acting maliciously in order to try and compromise the network).

PoS schemes based on PBFT, like the one described above, are generally invulnerable to attack as long as at least 2/3rds of the validators, weighted by stake, are honest, or non-byzantine and non-faulty. This guarantee is analogous to the guarantee in PoW systems that the network will remain safe as long as a malicious entity does not control 51% of the hash power.

Importantly, each block in a PoS scheme like the above involves much more communication overhead than for a typical PoW scheme. Whereas a PoW scheme only requires each validator/miner to receive a block, a PoS scheme requires that each validator not only receives the block, but also that they receive multiple rounds of votes from every other validator on the network. In practice, this has not been an issue for modern Proof of Stake networks, but it is a difference that is worth noting.

Faulty Leaders and Timeouts

In the previous section, we considered a stake-weighted mechanism to come to consensus on which blocks are valid. But we only considered the happy path where all validators behave as they're supposed to. Unfortunately, this is not always the case, and so PoS protocols generally need to add a few extra provisions for cases in which leaders fail to produce blocks in time, among other scenarios.

The two-phase core mentioned above ensures safety as it ensures no two validators will commit conflicting blocks at the same block height. However, consider the following situation where leader L2 is offline:

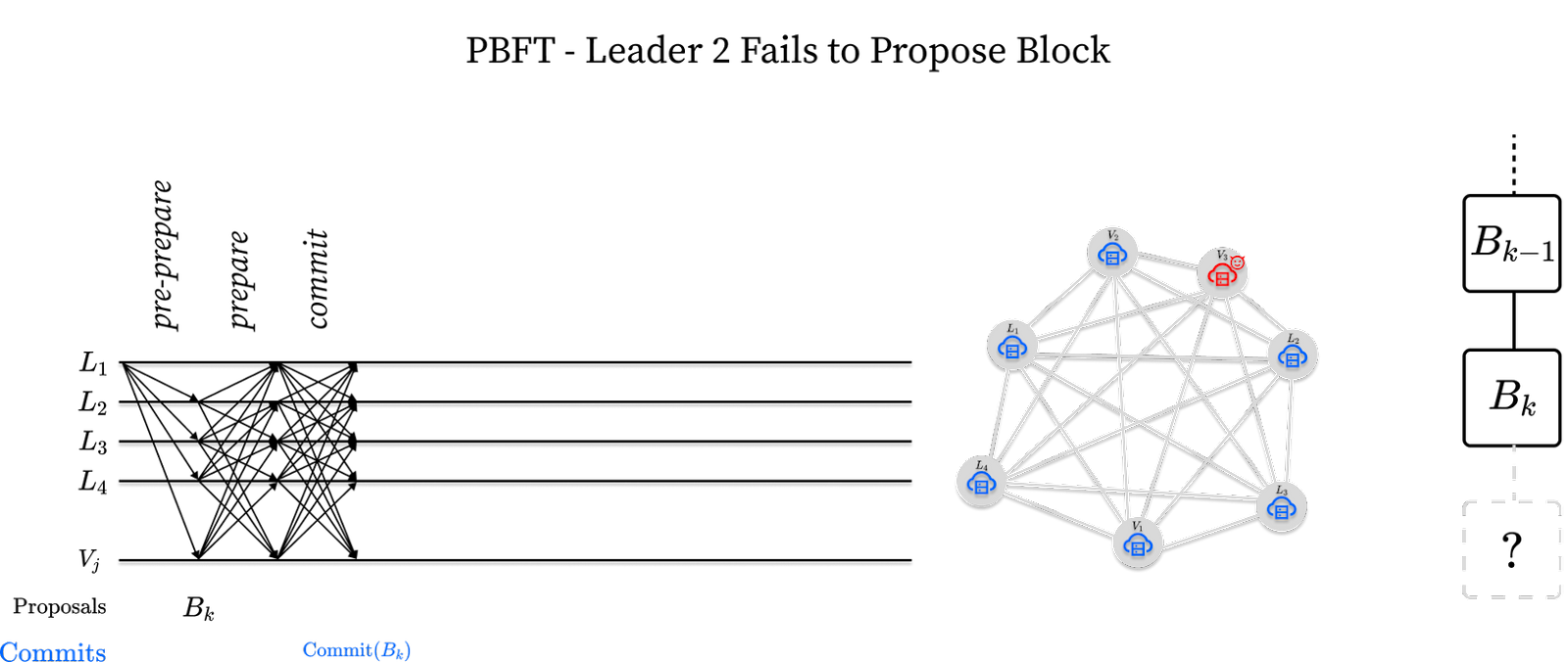
In this situation, leader L₁ successfully commits a block B_k but leader L₂ does not follow suit by proposing a block B_k+1. The network, if left alone, would permanently stall. The solution involves introducing a leader timeout. Validators are programmed to timeout after some time waiting for leader L₂. When a timeout occurs a validator sends a view-change message to all validators in the network declaring their intent to move to the next leader. On receiving a 2/3rds stake-weighted majority of view-change messages, leader L₃ can skip the previous round and propose a new block. This is depicted below:

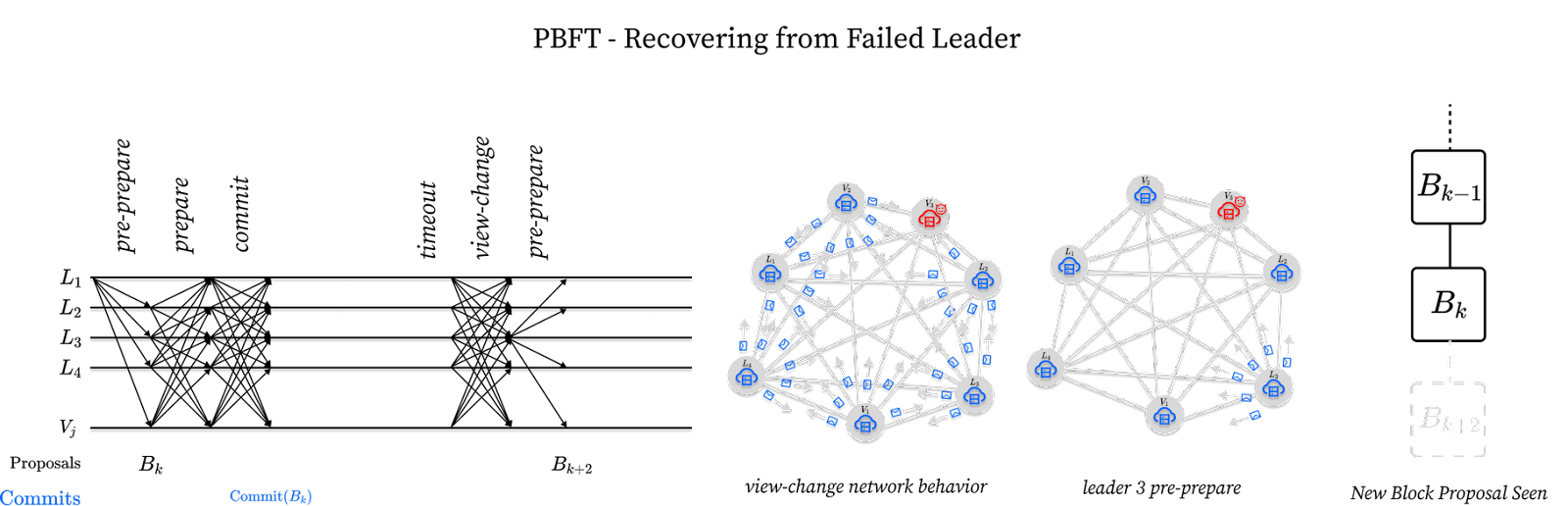
While this represents a simple scenario where all validators timeout the same leader at the same time by sending a view-change message to L₃, in theory the timeout scenarios can be much more complicated, hence why the proofs of PBFT protocols can get fairly involved.

To illustrate this complexity, consider an extreme situation where half the validators signal a timeout, i.e. a view-change, to leader L₂ while half the validators receive a valid block from L₂ and signal a timeout, i.e. a view-change, to leader L₄. While this seems like an extreme example, it could reasonably happen if a malicious leader were to intentionally partition the network by only sending their block to half of all validators, or if the network were to experience extreme issues, such as an internet outage. In these situations, leaders L₃ and L₄ would never be able to commit a block, as half the network expects the next block from leader L₃ and half the network expects the next block from leader L₄, and a 2/3rds majority is required to make forward progress. As such, every validator would timeout and the network would transition to half the leaders expecting a block from leader L₄ and the other half expecting a block from leader L₅. The way we've described the timeout mechanism above, without intervention, the network would never converge on a new leader and the network would effectively halt, or lose liveness.

To prevent this issue, PoS consensus protocols with round-by-round leader schedules require exponential backoff in their timeouts following the last committed block. Without going into too much detail, it is sufficient to understand that effectively doubling the timeout each time a node sends a view-change message results in the two partitions of the network eventually catching up to each other, rather than stalling indefinitely (proof available in Tendermint's paper here).

From Tendermint to HotStuff

The mechanism described previously gives a good foundational understanding of how a PoS consensus protocol can produce blocks. But it has two core issues that a new mechanism called HotStuff improves upon that we walk through below.

O(n²) -> O(n) Communication Overhead

First, in order for a block to be finalized in a PoS scheme like Tendermint, messages must be sent from each peer to every other peer. It would be much better if a single node could be assigned to aggregate these messages for each round, thus reducing the communication overhead from O(n²) to O(n).

We can achieve this by requiring that all pre-commit and commit messages are sent to every other validator, but rather only to the leader. This allows the leader to act as an aggregator of messages, thus reducing the communication overhead from O(n²) to O(n). The modified scheme looks as follows:

First, a leader is selected via a stake-weighted random sample of all validators. This leader bundles transactions into a block and sends this block to all other validators via a pre-prepare message like before.
After receiving a block, each validator sends their prepare message directly back to the leader rather than to every other validator.
The leader aggregates all of the prepare messages until they have received them from a 2/3rds of all validators, weighted by stake.
Once the leader has aggregated a sufficient number of prepare messages from validators, they send this aggregated bundle of messages to every validator.
- Depending on how this is implemented, the communication overhead of what the leader sends to all validators may technically still be O(n²), since the leader's message will contain O(n) prepare messages from validators. This can be reduced using a concept known as a threshold signature, which results in only O(1) information being communicated back per validator.
After receiving the bundled prepare messages from the leader, each validator sends their commit message directly back to the leader rather than to every other validator.
The leader aggregates all of the commit messages until they have received them from a 2/3rds of all validators, weighted by stake.
Once the leader has aggregated a sufficient number of commit messages from validators, they send this aggregated bundle of messages to every validator.
After receiving a bundled commit message from the leader, they finalize the block, making it so that no message from any other validator will ever revert the block or the transactions within it.

In practice, the above scheme achieves much better performance because the leader bundles validator messages together, rather than requiring each validator to send messages directly to every other validator.

Block Pipelining

Even with the above optimization, it is still the case that three rounds of communication are required to finalize each block, and that the finalization of the next block cannot proceed until these three rounds occur.

A natural optimization is to pipeline block finalization so that the round of voting on each block implicitly finalizes previous blocks. This not only results in a 3x reduction in the overhead required to finalize each block, but it also results in a conceptually simpler-to-describe mechanism that works as follows:

First, a leader is selected via a stake-weighted random sample of all validators. This leader bundles transactions into a block and sends this block to all other validators via a simple block-proposal message.
After receiving a block, each validator sends a simple vote message back to the leader, indicating that the block is valid.
- Importantly, the vote message replaces both the pre-commit and commit messages from the previous schemes.
The leader aggregates all of the vote messages until they have received them from a 2/3rds of all validators, weighted by stake.
Once the votes are aggregated, the leader forwards the votes in a bundle to the next leader. This bundle of votes is usually referred to as a Quorum Certificate, or QC for short, and it simply refers to the votes from 2/3rds of validators.
Once the next leader receives the QC from the previous leader, they propose the next block, and include the QC from the previous block within it.
A validator considers a block B_k-3 as finalized when it receives a QC for block B_k.
- Notice there is no fundamental difference between the commit rule for Chained HotStuff and the commit rule for Tendermint. Both still rely fundamentally on the concept of verifying that everyone has seen that everyone has seen a block. Chained HotStuff is just more efficient in its messages because it uses messages that indicate that a validator has seen block B_k to also indicate that the validator has seen that everyone has seen block B_k-1.

Chained HotStuff makes it so that every round of communication results in a finalized block, thus resulting in a 3x reduction in overhead required to commit each block.

To reach even higher throughput, Novi, a subsidiary of Facebook, introduced DiemBFT, which provided a simple optimization whereby validators send their votes directly to the next leader instead of sending them back to the block proposer.

While a minor improvement, such a scheme leads to higher throughput and lower latency for the network. Below is the communication footprint for DiemBFT. Notice the deliberate and structured communication pattern between validators and leaders. The assumption is that validators are in sync as to who will be the next leader and are capable of coordinating their messages as such.

Importantly, because DiemBFT introduces significant complexity over alternative schemes, without much benefit over simpler schemes, we will not be considering it for our implementation. However, it is useful to consider a diagram of what it looks like below, and to compare to Chained HotStuff from above:

Reducing One More Round with Fast HotStuff

Looking at Chained HotStuff, the commit rule indicates that a validator will finalize block B_k-3 when it receives block B_k. However, with a slight modification, we can reduce one more round of communication, such that a validator can effectively finalize block B_k-2 when it receives B_k. Moreover, we can do this without a significant increase in complexity.

Revolution achieves this by implementing an optimized state-of-the-art version of HotStuff called Fast HotStuff, which we describe in detail later on when we describe the Revolution consensus mechanism in detail.

Revolution Proof of Stake

Revolution combines several state-of-the-art innovations, listed in the introduction for reference, into one easy-to-understand and straightforward Proof of Stake protocol. In what follows, we explain all of the components of Revolution, effectively building up the protocol fully from scratch for a lay reader.

We start with how a new node syncs from its peers when it first joins the network, and then build up to how leaders are selected and blocks are produced and finalized in the steady-state. As we go along, we also cover other novel details like Revolution's burn-maximizing fee mechanism and its dynamic block reward scheme.

The Lifecycle of a Node

To fully understand Revolution and why it's important, it's important to understand the lifecycle of a node on the network.

Download and run the node software. First, one downloads the node software from the relevant repository and runs it.
- In the case of DeSo, one can either run a Rosetta node, as exchanges like Coinbase do, or a full node, as apps like Diamond and Openfund do.
- It is also important to mention that many apps like the DeSo Wallet app and the DeSo Chat Protocol demo app do not run their own node, but rather use the web2 APIs exposed by pre-existing nodes such as node.deso.org, which makes it much easier to build great user experiences.
Find other nodes to connect to (DNS Bootstrapping). Once the node software is running, the first thing it needs to do is find other nodes to connect to that it can sync from. This is done via a process called DNS Bootstrapping, which we discuss in detail in a subsequent section.
Download the current state from peers (HyperSync Bootstrapping). Once the node has found a set of valid peers to connect to, it needs to get its state up-to-date with that of its peers.
- Put simply, every node on the network needs to have a consistent view of all account balances and, in the case of DeSo, all content as well such as posts, follows, NFTs, etc...
- The DeSo blockchain has an extremely efficient syncing method known as Hypersync Bootstrapping, which we will discuss in detail in a subsequent section. Simply put, Hypersync allows a node to first download a snapshot of the existing state from its peers, i.e. all balances and content, then sync blocks up to the tip thereafter. This is much faster than having to sync all blocks from the beginning of time, like many other protocols do.
Become a validator - optional. Once a node is fully up-to-date with all of its peers, it can either passively receive transactions (via blocks) and commit them to its state to stay up-to-date, or it can become an active participant in consensus called a validator. The process of becoming a validator will be described in detail in subsequent sections, but a preview is below.
- In order to become a validator, a node must first register itself with the network by submitting a transaction containing a public key, which will be used to identify it as a validator.
- Once a node has registered itself as a validator, anyone can stake coins to this node, allowing it to have more weight as a participant in the network. We will go into all the details of this in subsequent sections.

Participate in consensus - optional (Fast Hotstuff). Once a node has become a validator, with some stake assigned to it, it can now participate in the process of bundling transactions into blocks and voting on blocks, causing the transactions within them to be committed to the state of all nodes on the network.
- Revolution relies on a particular consensus algorithm to achieve this called Fast Hotstuff, and we will discuss how the process of proposing and finalizing blocks works in subsequent sections.

Of course, Revolution adds various twists to this process when compared to other protocols, such as introducing the concept of revolt among nodes on the network, and introducing a burn-maximizing fee model, among other innovations.

The above being said, this basic context is really all a node on the network will be doing at the high level. The rest of this document will just focus on the details of each step, starting with finding peers and working our way up.

Netboot: Censorship-Resistant DNS Bootstrapping

The first step when a node comes online is to find peers that it can connect to. But this is a trickier problem than it sounds. After all, if you've just downloaded the software for your node and run it for the first time, then you won't know who's online for you to connect to. The situation is not dissimilar to moving to a new town where you have no pre-existing relationships.

Hardcoding bootstrap peers: The most obvious way is to hardcode a list of peers into the software that node operators download. The problem with this is that updating the list of peers requires a centralized decision to be made by the development team, and then also requires everyone to download the latest copy of the software, which is very cumbersome.

Naive DNS bootstrapping: The way that software like Bitcoin solves the problem of hardcoded peers is that the software hardcodes a list of domains, such as seed.bitcoin.sipa.be. This allows the list of bootstrap peers to be updated without needing a centralized decision to be made by the developers and without needing everyone to update their software. Instead, you just need one of the owners of a trusted DNS bootstrap domain to update their DNS records to add a new peer. Once this is done, everyone who runs the software will query this peer when they first boot up.

You can actually see the list of DNS bootstrap domains for Bitcoin Core in their GitHub repo here. Cool right?

The problem with the naive DNS bootstrapping approach is that it's still highly-centralized because you need the operator of one of the trusted DNS bootstrapping domains to make a decision in order for the bootstrap list to be updated. Wouldn't it be nice if anyone could add themselves to the list of bootstrap peers at any time? This is what we solve with a new DNS bootstrapping approach we call Netboot.

Netboot censorship-resistant DNS bootstrapping: With Netboot, instead of relying on a fixed set of hard-coded DNS bootstrapping domains, nodes are programmed to scan a wide field of domains based on a prefix. We explain this with an example below.

Consider an example where a node is hard-coded with the Netboot prefix revolution-seed-[0-9]*.io. A node implementing the Netboot approach would begin scanning every domain that satisfies the prefix, starting with revolution-seed-0000000.io and finally finishing at revolution-seed-9999999.io. It then would treat each domain as a DNS bootstrapping domain. The advantage of this approach is that anyone can buy a domain that satisfies this pattern and be added to the set of bootstrapping domains without needing approval from a centralized set of people.

As long as the space of domains is sufficiently large, it would be prohibitively expensive for one entity to purchase all of the domains in the space. Moreover, as long as a single valid domain exists in the set of domains being scanned, the node will eventually find a valid peer to begin syncing from, and it can move on to the next phase of bootstrapping.

HyperSync: Efficient Snapshot Bootstrapping

Once a node has found a valid peer to sync from, it moves on to the next phase of bootstrapping: HyperSync. In this phase, the node downloads a snapshot of the current state from one of its peers and verifies that this snapshot is consistent with what it is seeing from other peers via a novel checksum algorithm we call Elliptic Sum, which we'll explain in this section.

Before we go into explaining HyperSync, it's useful to first understand how more traditional blockchains like Bitcoin get up to speed. In Bitcoin, new nodes must download and verify the full history of transactions since the very first block in order to be able to process transactions and participate in the consensus process. This can take a long time, and is a major bottleneck for new nodes joining the network.

In contrast, HyperSync allows new nodes to get up to speed much faster. This is because instead of downloading the full history of transactions, nodes only need to download the latest snapshot of the network state, and then transactions from the snapshot block height to the tip of the blockchain (i.e. the most recent block that has been broadcast to the network).

The snapshot contains the current state of the ledger (including all balances and content), and the current validator set. With this information, the node can quickly verify the integrity of the current state of the network and start participating in consensus without having to download and verify all transactions from the beginning of time.

Elliptic Sum

One major key to HyperSync's performance is the Elliptic Sum checksum which DeSo describes in its full implementation details here. Elliptic Sum is a checksum generated by each node which verifies the consistency of the snapshot across multiple peers.

Simply put, if two nodes have exactly the same snapshot state, then the Elliptic Sum value for each of them will match. Otherwise, if even a single byte of their snapshot state differs, then they will have a different value for their Elliptic Sum.

When a node downloads a snapshot from a peer, it calculates the Elliptic Sum checksum for that snapshot. It then compares the checksum to the checksums calculated by other peers. If the checksums are all the same, the node knows that the snapshot is consistent across peers and can trust that it is up-to-date. This allows it to start participating in consensus without needing to download the full history of the blockchain.

Performing an integrity-check like this is critical, as without it a nefarious node could trivially sneak a malicious balance into its state with millions of coins in it. This would be especially costly if your node is powering an exchange like Coinbase.

The main breakthrough that Elliptic Sum introduces over other approaches is its speed and its space-efficiency. In particular, while other protocols like Ethereum and Solana support a "fast sync" option, the integrity-check portion of their sync requires them to compute a merkle tree of all values in their state (a good explainer of merkle trees here).

Merkle trees not only double the storage requirements of a node, but they also result in every state change requiring many random hops through disk to modify the merkle tree up to its root. For this reason, Solana and Ethereum are both notoriously slow at processing state changes, and have extremely high storage requirements for full node operators.

In contrast, DeSo nodes, which implement Elliptic Sum, incur only a 32-byte overhead for their integrity-check, and updating the checksum is done in constant-time, with no disk-hopping. This constant-time update combines with Ancestral Records, which we'll discuss in the next section, to produce truly breakthrough node efficiency, especially from a content storage standpoint.

Ancestral Records

Concretely, nodes produce and store snapshots at known intervals, say one snapshot every week. These intervals are expressed in a number of blocks, so if Revolution produces a block every 3 seconds, then nodes would produce a snapshot roughly every 201,600 blocks (1 week expressed in a number of blocks). This snapshot interval would be common across nodes so that checksums for known block heights can be easily compared.

The naive way to produce a snapshot would be to simply store a full copy of the entire state at each interval. While this would be incredibly costly from a space-efficiency and computation standpoint, and arguably prohibitive for chains that intend to store a significant amount of content, most protocols actually do something naive like this to support their "fast sync" approaches.

In contrast, HyperSync utilizes a very clever scheme called Ancestral Records, described in detail here, which allows it to only store the changes between the snapshot height and the tip.

In particular, every time the state is modified after a snapshot, the old record is stored so that it can be used to recompute the snapshot from the "tip" state at will. At any block height after the snapshot, the full snapshot state can be derived by taking the current state at the tip and effectively merging it with the ancestral records. Then, once the node reaches a new snapshot interval, it just needs to delete all of its ancestral records and start creating deltas from the new snapshot height.

This results in a radical improvement in space-efficiency when compared to other approaches to node snapshotting.

Putting it All Together

Elliptic Sum's constant-time constant-space checksum scheme combines with Ancestral Records to produce a truly breakthrough snapshotting scheme from a storage-efficiency standpoint. In particular, because Elliptic Sum's update is constant-time and constant-space, it is virtually free to keep and update a checksum for each state snapshot. In particular, every time a value in the state is modified, both the snapshot checksum and the tip checksum can be modified in constant-time, and incur an overhead of only 32 bytes each.

The inefficiency of alternative schemes for producing new snapshots at regular intervals, and keeping their checksums up-to-date, presents a natural ceiling on how much data a blockchain can reliably store. For example, if a node is naively making a full copy of the state every time it produces a snapshot, or even if it's modifying cumbersome merkle trees on every write, then it effectively needs to be able to pause all on-chain activity for the amount of time that it takes to do those operations. Such a scheme would naturally not be able to manage an amount of content from a social graph the size of Instagram or Twitter, as the full copy would take a prohibitive amount of time, potentially days, and hopping around disk on every write to compute a checksum would likely become prohibitively expensive (and potentially require cross-machine communication for every single write).

As such, partially as a result of Elliptic Sum's breakthrough space-efficiency gains over merkle trees, and Ancestral Records' breakthrough space-efficiency gains over naive full-copy snapshotting, the DeSo blockchain is capable of storing one gigabyte of data for about $80, while Solana costs about $1.3 million for the same amount of storage, and Ethereum costs about $393.7 million (calculations here). We believe this is due to the fact that the natural ceiling for what DeSo is capable of storing is significantly higher.

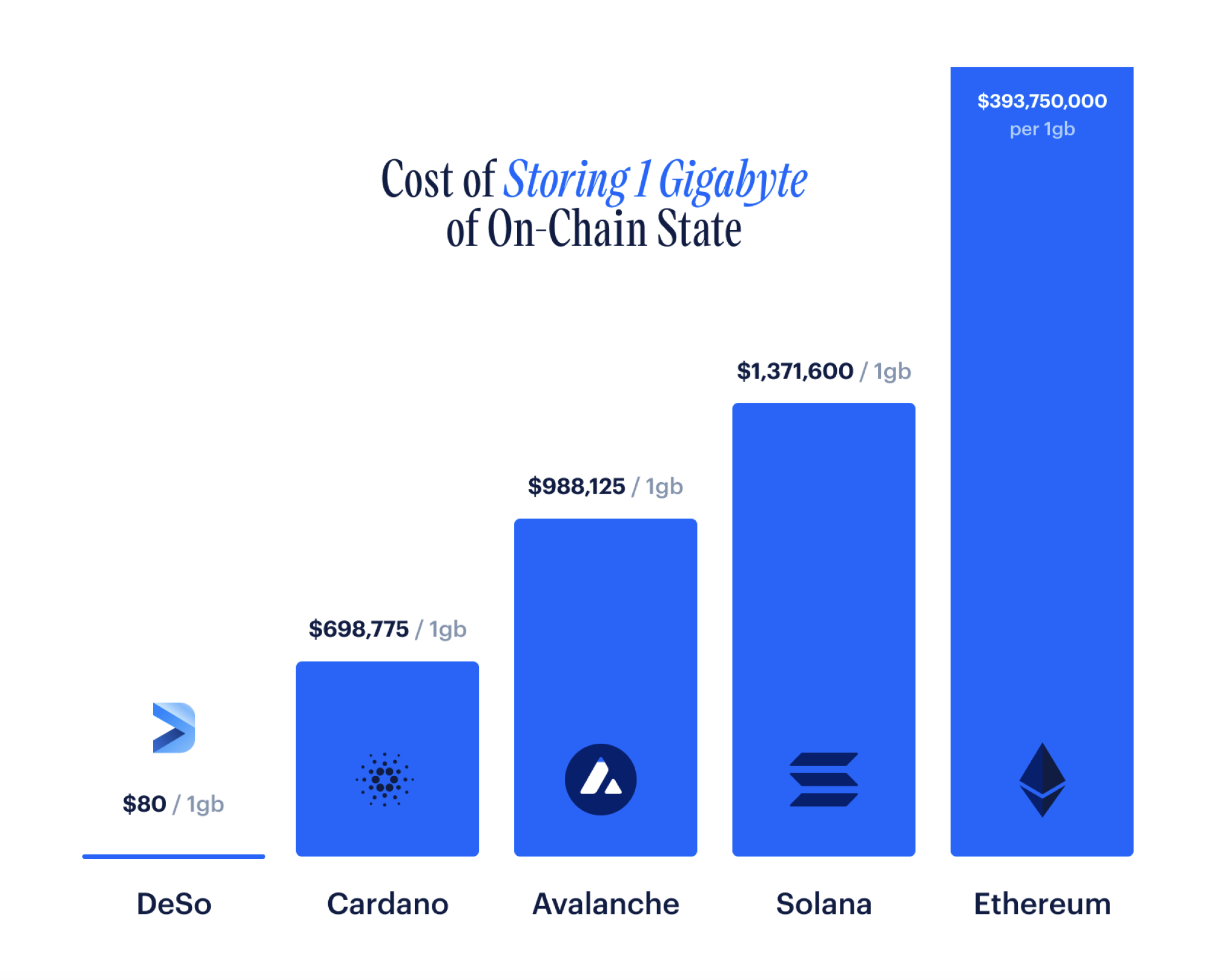
In summary, HyperSync is a novel way of bootstrapping a node quickly and securely, allowing new nodes to join a blockchain network and start participating in consensus much faster than they could with traditional blockchains.

For a deep-dive on how HyperSync, Elliptic Sum, and Ancestral Records work, check out DeSo's full description of its implementation here.

Sovereign Staking (a.k.a. No-Lockup Staking)

Once a node is fully in-sync with its peers, it can automatically begin to receive blocks, check their validity, and commit them if it finds them to be valid. However, in addition to passively receiving blocks, a node can also become an active member of consensus by becoming a validator. We describe what that looks like in this section.

Registering as a Validator

DeSo’s Proof of Stake protocol is permissionless, meaning any user can register as a validator to help secure the network at any time. To register, a user submits a transaction to the network telling other nodes that they want to participate in consensus. When a user submits a RegisterAsValidator transaction, they provide roughly the following information:

Their public key
An ordered list of domains where their node(s) can be reached for sending and receiving protocol-related messages
A flag indicating whether or not they will accept delegated stake, i.e. stake assigned to them by other users

Once this transaction has been validated and accepted by the network, the node is now a registered validator and stake can be added either directly by the user (self stake) or, if allowed, by other users (delegated stake).

If the user decides to remove themselves from the validator set, they can submit an UnregisterAsValidator transaction to the network. This will automatically return all of the validator’s stake to each staker and remove the validator’s eligibility to participate in consensus.

A benefit of a decentralized network is that there is no single validator who is a single point of failure. If a validator unregisters, the network continues to produce blocks as before with zero downtime.

As a safety check, Revolution requires a cooldown period of approximately three hours (three epochs, as we'll discuss) between a validator registering and unregistering to prevent users from trying to flash-stake or arbitrage some leader schedule opportunity by quickly registering, staking, and unregistering. Revolution also implements additional safety mechanisms against this via an unstaking lockup as well, explained in the Unstaking section below.

Staking

Any user can provide stake to an existing validator, either to their own node or, if allowed by the validator, to a third-party validator who accepts delegated stake. To stake coins with a validator, a user submits a “Stake” transaction to the network specifying roughly the following values:

The staker's public key
The public key of the validator they want to stake to
The number of coins they would like to stake

The coins are removed from the user’s wallet and held in escrow while staked with the validator. Importantly, the validator never takes custody of any delegated stake, so it is impossible for a malicious validator to run away with any delegated stake. This means that any staked funds are secure and not reliant on any trust with the validator. Staked coins are never accessible to the validator, instead they are only accessible to the staker directly and only if unstaked and unlocked.

The user can increase their stake position either with that validator or with any other eligible validator by simply submitting another Stake transaction. A user can stake up to 100% of the coins held in their wallet (net any transaction fees required to retrieve their funds). Staking is an easy and secure way to passively receive a reward for securing the network, as discussed in the next section.

Block Rewards

Any registered validator with non-zero stake is eligible for block rewards. Refer to the Dynamic Block Rewards section for more information on how block reward amounts are determined. The recipient of the block reward is randomly chosen (weighted by stake) using Collaborand, Revolution's on-chain randomness generator, as the seed for the random sample. In this way, the block rewards a validator can expect are proportional to the amount staked with them. The leader also receives a small percentage block reward to incentivize their responsibilities to construct and broadcast satisfactory blocks as well as compile other validator votes approving the block.

By design, Revolution does not include any slashing mechanism, and it does not require any stake to be locked up for long periods of time, as will be discussed in the Unstaking section. This is a major advantage for validators who are concerned about intermittent downtime putting their stake at risk, as is the case with other protocols. Instead, leaders who fail to propose a block and/or validators who fail to vote on a block are simply not eligible for block rewards. This incentivizes all leaders and validators to follow the rules of the protocol if they want to receive block rewards, while not placing their original stake at risk. If a malicious leader chooses to delay submitting a block, they will timeout, lose out on potential block rewards, and the protocol will continue unabated with the next leader in the leader schedule. If a malicious validator refuses to vote on blocks, they will similarly be ineligible for any block rewards.

With each block that gets accepted by the network, a block reward is assigned to a random validator. The protocol does not enforce the mechanism by which validators subsequently split up block rewards to be distributed among their delegated stakers. This gives validators an axis of competition across which they can compete for delegated stakers, attracting new stakers by minimizing their fee for operating a node and maximizing the block reward percentage flowing back to the stakers. Stakers will then be able to choose a validator comparing their relative fees in the Validator Hub (see section below). Stakers can have their block rewards automatically restaked, by issuing a derived key to the validator granting the validator permission to issue Stake transactions on their behalf. This is a major advantage over other protocols which require block rewards to be manually claimed by stakers and manually restaked on some cadence.

Unstaking

A user with staked coins can unstake up to 100% of their stake with any validator by submitting an Unstake transaction to the network specifying roughly the following information:

The staker's public key
The validator’s public key
The amount to be unstaked

Unstaking immediately removes the specified stake from the validator and will immediately impact stake-dependent calculations for the validator such as their chances of receiving a block reward and their placement in future leader schedules. The funds will not, however, be immediately available for withdrawal by the user. There is a brief lock-up period (lasting two epochs, or two hours, as we will discuss in a later section) during which the funds are held in escrow, neither staked with the validator nor accessible by the user. Once the brief lock-up period has passed, the user can submit a second UnlockStake transaction to the network whereby their funds will be returned automatically to their wallet.

The purpose of this lock-up period is to prevent leader schedules from becoming gameable by malicious stakers quickly adding and removing stake. As explained in more detail in our Line of Succession Leader Scheduling section below, leader schedules are determined two epochs in advance and unstaked funds are locked for two epochs. This ensures that there cannot be any flash-staking operations to try to manipulate the leader schedules. The leader schedule is guaranteed to reflect all stake currently assigned to each leader during the epoch in which that leader schedule is in effect. A user can submit multiple Unstake transactions to unstake incremental funds from the validator, or funds from multiple different validators.

Validator Hub

To promote decentralization of stake among validators and transparency of block rewards and fees, Revolution will have a Validator Hub application (e.g. validators.deso.com) where users can easily shop around registered validators, search and filter for certain attributes, track their accumulated block rewards, and increase or decrease their stake positions. See screenshot below.

Fast HotStuff In-Depth

Until now, we have described how a node gets in sync with the rest of the network, and how validators accumulate stake. This base level of understanding is now sufficient to start discussing what validators actually do to produce and vote on blocks, and the process by which transactions are finalized. Going forward, we will assume the reader is familiar with all of the concepts outlined in the Background section previously.

The Gist of Fast HotStuff

Revolution uses a version of consensus called Fast HotStuff that is very similar to Chained HotStuff, as outlined in the Background section.

The core insight that Fast HotStuff makes when compared to Chained HotStuff is the realization that there is some room for optimization with regard to how nodes timeout faulty or malicious leaders. In particular, by introducing an explicit timeout message to the original Chained HotStuff protocol, Fast HotStuff effectively makes it safe to commit one block earlier than was previously possible.

We include the full pseudocode for Revolution's implementation of Fast HotStuff in the next section, but it's valuable to consider a rough sketch of the pseudocode below, and to compare it to Chained HotStuff, which has a sketch in the Background section, and which we've also included pseudocode for in the next section:

First, a leader is selected via a stake-weighted random sample of all validators. This leader bundles transactions into a block and sends this block to all other validators via a simple block-proposal message.
Then, a validator can do one of two things:
If the validator receives the block within the timeout window and the block passes their validation checks, then they send a simple vote message to the next leader, indicating that the block is valid.
However, if the validator does not receive a valid block within the timeout window or the block is invalid, then they send a distinct timeout message to the next leader.

At this point, two things are happening in parallel:
- The next leader, who is ready to produce a block, is working on aggregating enough votes to make a VoteQC (2/3rds of all validators weighted by stake). If they reach this point, then they embed the VoteQC in their newly-constructed block, and broadcast this block to all validators.
- The next leader is also listening for timeout messages from all validators. If they get timeout messages from 2/3rds of all validators weighted by stake, then they use these messages to construct a TimeoutQC, which they can also embed into a newly-constructed block. In this case, their block containing the TimeoutQC will be the next block in the chain, and the faulty leader before them will be skipped.
A validator considers a block B_k-2 as finalized when it receives a VoteQC for block B_k.

This description is missing some nuance with regard to how blocks are committed and what happens during timeouts, which the pseudocode covers. Additionally, proving that this mechanism always works requires a detailed proof, which we'll refer the reader to here (original paper here). This being said, the sketch above is roughly similar to what an actual implementation would do, and it illustrates how a round of communication can be removed without significantly increasing complexity.

Fast HotStuff Pseudocode

In order to truly understand HotStuff and Fast HotStuff, including all the nuance in how vote and timeout messages are processed, we feel the best way is to browse some simplified pseudocode that we wrote for each algorithm. This pseudocode attempts to capture every edge-case in the protocol's timeout scenarios, without adding any more complexity than what is strictly necessary. You can see the full repo with all the pseudocode here. Each implementation is also linked below for convenience.

chained_hotstuff.go: This is an implementation of the basic chained hotstuff algorithm, which requires three rounds of communication in order to finalize a block. It's useful to start here in order to get a sense of what the basic algorithm looks like.
- The key thing to note about this algorithm is that it does not include information about previous timeouts in its blocks, which is the core optimization that fast-hotstuff adds, which subsequently allows fast-hotstuff to cut finalization time down to two rounds instead of three.
fast_hotstuff.go: This is an unoptimized version of the Fast HotStuff consensus algorithm. It is unoptimized in the sense that it does not aggregate signatures, which we think makes it easier to understand what information needs to be sent between validators. Notice that the code follows the high-level gist given in the previous section, but with many nuances fleshed out, such as how timeout messages are aggregated by the leader.
fast_hotstuff_bls.go: This implementation uses BLS signatures instead of vanilla signatures to optimize the previous implementation. In particular, whereas the previous implementation may end up requiring O(n^2) messages to be sent to propose a block, this implementation achieves the theoretically-optimal O(n) complexity. In addition, note that the implementation attempts to fully explain the important details of BLS via the comments so that you don't need to be familiar with BLS signatures to understand how it works (though we also include some helpful information in the next section).

We have done our best to make it so that the pseudocode can be read in one pass from top to bottom, without needing to hop around too much. We have also aimed to thoroughly annotate the pseudocode implementations with an ample quantity of comments.

If anything seems confusing, or if you have any questions, we encourage you to create an issue on the GitHub repo.

A Note on BLS Signatures

BLS signatures are used to effectively compress signatures from N different validators into a single signature value. While we won't go into too much detail on how they work here, we do want to cover some of the important properties that make them favorable in a PoS scheme like this.

Setup. BLS signatures require a "setup" phase in order to work. This amounts to adding a field to RegisterAsValidator that allows one's public key to be used as a participant in the BLS scheme.
Partial signatures. When an individual validator signs something, we refer to that in the pseudocode and more generally as a partial signature. We call it this because it can be combined with other partial signatures to form a combined signature.
Combined signatures. If you have N signatures that have all signed the same payload, i.e. if you have N partial signatures, those signatures can be compressed into a single signature that we refer to as a combined signature. The combined signature is the same size as a single partial signature. If one is familiar with elliptic curves, this amounts to adding N elliptic curve points, which is very efficient.
- There is one very important caveat, however, which is that verifying the signature requires knowing which public keys participated in the combined signature. For this reason, BLS signatures in Revolution come bundled with a bitmap that uses one bit to represent each known validator that is currently participating in consensus. The bit is 1 if the validator participated in the signature, and 0 if they did not.
- Note that this is highly-efficient because even if there are 10,000 validators included in a bitmap, this comes out to only about a kilobyte.
Verifying a signature. In order to verify a signature, the verifier must first compute the public keys of all of the participants using the bitmap mentioned previously. The verifier then adds the public keys together, which is very efficient, into a group public key. This group public key can then be used to check the aggregate signature.
Efficiency. Obviously, a BLS signature is much more space-efficient than including N distinct signatures into a message. But BLS signatures are also much more computationally efficient as well. In particular, even though a BLS signature bundles N signatures together, it is much more efficient than checking N signatures individually. This is because the act of combining public keys, as mentioned in the previous bullet, is much cheaper than the act of actually checking that a signature maps to a particular public key.

If you understand the above properties of BLS signatures, you should have everything you need to process the pseudocode for Fast HotStuff with BLS.

Line of Succession Leader Scheduling

A consensus mechanism like Fast HotStuff is typically paired with a leader selection scheme that defines which leader is going to be producing a block for each view. This is the abstracted computeLeader function in the pseudocode from the previous section.

Leader selection schemes usually utilize some form of on-chain randomness, which we will cover in the next section, to assign a particular leader to each view. This random leader schedule is computed identically across all validators, typically well in advance, so that for any given view, every validator is fully in-sync with all of its peers about who the leader is.

As a concrete example, a very simple leader selection scheme could be to use the block hash at every thousandth view as a random seed to generate an assignment of leaders to views for the next thousand blocks. For example, imaging if the leader for block N was simply:

BLOCK_HASH(N-1) % NUM_LEADERS

There are several issues with this scheme, including the fact that the block hash is not a robust source of randomness. But hopefully it communicates the gist of how other protocols compute leader schedules.

A major problem with virtually all approaches to computing leader schedules is that the resulting leader schedule switches rapidly between leaders on every block. This constant switching has several issues, the biggest of which is that it results in a significant throughput and latency hit.

Revolution presents a breakthrough leader selection process that we call Line of Succession Leader Scheduling that drastically improves performance without compromising on censorship-resistance or decentralization. We describe this process in detail in this section.

Election and Line of Succession

Revolution introduces a novel approach for leader selection that we call Line of Succession Leader Scheduling. This leader selection approach improves network throughput and transaction finality time by designating a single node as the block proposer for a one hour term, and having them remain in their role until they finish out the term, time out, or the network revolts against them due to censorship.

The Line of Succession Leader Schedule uses a lottery of the top m validators by stake to produce a stake-weighted random ordered list of validators. Each validator appears no more than once in the list. A new list is produced once every hour, and defines the line of succession for an upcoming one-hour term.

The list of validators is used as a leader line of succession for a one-hour term. The first validator in the list is elected as the leader for that one-hour term. They remain the leader until they successfully reach the end of the term, until they time out, or the network revolts against them. In the event of a timeout or revolt, the protocol falls back to the next validator in the line of succession. The next validator becomes the new leader until they peacefully reach the end of the term, or until they too time out or are revolted against. If the protocol reaches the end of the list, it loops back to the beginning, giving everyone another chance to finish the one-hour term.

Mechanics of The Election

The protocol uses a concept of an epoch to represent each one-hour term. An epoch is defined as a range of blocks with known starting and ending block heights. The range of blocks is configured such that an epoch lasts roughly 1 hour during normal network conditions (3600 blocks). A new epoch can begin only when the 3600 blocks for the previous epoch have been finalized.

The election runs every time the protocol finalizes the last block in an epoch. The election at the end of epoch e_n produces the leader schedule for epoch e_n+2, two epochs in advance. Concretely, the election process works as follows. Assume we have four validators, with varying stake:

Validator L₁, which has 600 DESO staked
Validator L₂, which has 300 DESO staked
Validator L₃, which has 100 DESO staked
Validator L₄, which has 50 DESO staked

When finalizing the last block at the end of epoch e_n, the protocol takes a snapshot of the top m validators by stake. The top m validators are all eligible to be leader for epoch e_n+2. Assuming m=3 in this example, this means that validators L₁, L₂, and L₃ are all eligible to be leaders in epoch e_n+2. Validator L₄ is not eligible to be leader for epoch e_n+2. Note that restricting this process to the top m leaders is not strictly necessary, and that m will be fairly large in practice, e.g. 1,000.

L₁, L₂, and L₃ are then entered into a stake weighted lottery to determine the first leader for epoch e_n+2 and then to determine order for the line of succession. The sum total of the stake among the top 3 validators is 1000 DESO, with L₁ having 60%, L₂ having 30%, and L₃ having 10%. These percentages reflect each validator’s chance of being selected as the first leader in epoch e_n+2, and also reflect each validator’s relative stake weight amongst each other.

The protocol then uses staked weighted sampling without replacement to produce an ordered list forming the line of succession for epoch e_n+2. Every permutation of the L₁, L₂, and L₃ is valid, and has a chance of occurrence in line with the probability of the occurrence of that permutation. Example:

L₁ → L₂ → L₃ (45% probability)
L₂ → L₁ → L₃ (25.71% probability)
L₁ → L₃ → L₂ (15% probability)
L₃ → L₁ → L₂ (6.67% probability)
L₂ → L₃ → L₁ (4.29% probability)
L₃ → L₂ → L₁ (3.33% probability)

This approach results in a process in which leader schedules are always known up to two epochs ahead of time (up to 2 hours). Over many epochs, this also results in leader schedules where every validator has a chance to be a leader in proportion to its relative stake.

Performance Advantages

While having a static leader and leader schedule in each epoch is a constraint, we believe that Line of Succession Leader Scheduling will result in network performance wins without compromising on censorship resistance. The line of succession mechanism in each epoch ensures that the network will always converge on the first leader that is able to propose and finalize blocks in line with the protocol’s latency, throughput, and censorship resistance requirements.

In normal network conditions, in which the current leader is able to meet the protocol’s requirements, all validator nodes can maintain direct open connections with that leader for the duration of the epoch. In contrast with other leader selection approaches that have frequent changes to the current leader, this has two advantages:

It eliminates the need for additional network handshakes needed for validators to connect to the leader.
It reduces the overall number of round-trip P2P messages needed to propose and vote on blocks in the steady-state.

In adverse network conditions, in which multiple leaders in an epoch are not able to meet the protocol’s requirements, this approach can reduce the total time the network spends on such leaders during that epoch. This is best demonstrated by a concrete example.

Assume we have the leader succession list L₁ → L₂ → L₃ for an epoch. Now assume L₁, and L₃ are both offline, leaving L₂ as the only live eligible leader for the epoch. The protocol will start with L₁ as the leader. Once L₁ fails to propose a block, the network transitions to L₂ who can remain leader until the end of the epoch. This allows the protocol to avoid ever transitioning to L₃ or back to L₁, minimizing the total time spent on faulty leaders during the epoch.

In contrast, with the more traditional random leader selection schemes used by other protocols, the network would experience timeouts on 2/3rds of all views for which L₁ and L₃ are the randomly selected leaders.

Network Configuration

In this section, we propose initial values for the election's parameters. This being said, note that the election’s parameters are configured as global parameters for the network, which are updated via decentralized on-chain amendments. See the section on on-chain amendments for details on how these values are updated.

Eligibility for Leadership

In order for a node to be eligible to be leader for an epoch e_n+2, it must satisfy two requirements at the end of epoch e_n

The validator node must have the minimum amount of DESO staked on themselves (100 DESO)
The validator node must be ranked in the top 1,000 validators by stake

Epoch Duration

Epochs are tuned to a duration of about one hour during normal network conditions. Assuming the network can finalize blocks in the steady-state every 1 second, this means it will finalize roughly 3600 blocks per hour. The epoch length is initially configured to 3600 blocks to meet this.

Timeouts and Timeout Duration Exponential Backoff

A validator may time out a leader if the leader fails to propose a valid block within a reasonable amount of time. This duration is configured to 30 seconds.

The result of a revolt on a leader, which we will discuss in a later section, also matches that of a timeout. In the event of a timeout or a revolt, a validator transitions to the next leader and increases the duration with which it waits for a valid block to 60 seconds.

In the event of many consecutive timeouts or revolts with no block finalization in between, validators employ a 2x multiplier for the exponential backoff to increase the durations:

30 seconds → 60 seconds → 120 seconds → 240 seconds → …

The 2x multiplier ensures in the event of extended network outage, multiple node restarts, successive misbehaving leaders, etc... that the network will eventually converge on the same leader.

Solorand & Collaborand - Robust On-Chain Randomness

On-chain randomness is a critical feature of any PoS blockchain, and it refers to the concept of generating a random seed, known to all validators on the network, usually with every block, that can then be used to generate random events.

On-chain randomness is usually most useful in PoS settings for defining an un-gameable leader schedule. For example, without on-chain randomness, the leader schedule would be potentially manipulable by a single entity or group of colluding entities. But on-chain randomness can be used for many other things, including as a random seed for smart contracts that need a source of randomness in order to function.

Why On-Chain Randomness is Hard

Even though on-chain randomness is critical to every PoS scheme, it is one of the hardest things to get right. What makes it so hard? The reason is that it's very easy to accidentally introduce a flaw into a randomness scheme that allows a single entity to grind or skew the randomness significantly. To understand this, it's useful to walk through a few randomness schemes that don't work, and to understand what makes them flawed.

Strawman #1: Block hash. Imagine using the hash of each block as the protocol's source of randomness. What could go wrong with that, right? The problem is that in PoS schemes, the hash can be manipulated by the leader simply by changing the contents of the block, e.g. by reordering votes from validators.
- In particular, because votes from validators can appear in any order in the block, the leader has N! permutations of vote orderings to grind through in order to manipulate the block hash into being whatever they want. This means that, with just a little iteration through vote orderings, a leader could assure that they would be at the top of the leader schedule forever!
- Even if vote ordering is fixed, the leader can still game the randomness by omitting votes, reordering transactions, or even simply submitting a transaction of their own with a nonce that they can grind through.
Strawman #2: Pooling hashes. Imagine you want to eliminate reliance on a single validator in your randomness computation by inventing a scheme that combines randomness from N different validators. Imagine a scheme whereby all validators are allowed to submit hashes to a pool each block, and then all the hashes are combined to form a single random seed for a block (imagine the leader can't censor here). At first glance this seems more promising than the previous scheme because a single leader acting honestly ostensibly makes the seed computation random. But there is a fatal flaw with this scheme as well.
- Since PoS mechanisms operate in the open, everyone can see the random hashes that are being pooled before they are finalized into a block. Because of this, any malicious validator can grind their own randomness to skew the outcome to whatever they want.
- For example, suppose you want the pool to compute outcome X (e.g. maybe X is chosen as leader in the next block). Well, the pool's output depends on your input, since it's technically computed as Hash(poolRandomValues || yourRandomValue). Because of this, you can try all values of yourRandomValue until the overall outcome is exactly what you want.
Strawman #3: Commit reveal schemes. One way around the grinding problem, employed by RanDAO, which is utilized by Ethereum, is to implement a two-phase commit-reveal scheme. In such a scheme, each validator submits a hash of their randomness in the first phase, and then submits the actual value of their randomness in the second phase, which is checked against the hash in the first phase. The values from the second phase are then combined to create the randomness. Can you see an attack here?
- Imagine you create just ten malicious validators. Your validators submit hashes in the first phase, but selectively censor their reveals in the second phase based on what people reveal as their randomness. With just ten validators, this gives you the ability to choose from 2^10 possible outcomes to grind over for every cycle based on whether you choose to reveal in the second phase!
- RanDAO attempts to mitigate this by requiring a pledge from people who participate in the randomness scheme. This pledge is then slashed if people don't reveal in the second phase. While this may solve most of the problems in practice, it has the downside of being expensive to run (because you need to incentivize people to take the risk of losing their pledge) and still game-able if one is willing to lose a few pledges to manipulate the randomness.

Desirable Properties

Having walked through three flawed approaches, it is useful to describe what we want from our randomness scheme.

Ungrindable. This property refers to the inability of any network participant to skew the outcome of the randomness generation algorithm. With ungrindability, there is no strategy that malicious validators can exercise to influence the randomness in their favor.
Unpredictable. By this property, we mean that no validator can foresee what the randomness will look like in the future. Unpredictability does not necessarily mean that all validators will learn of the randomness at the same time – this is likely an unsolvable proposition. Instead, we only require that no validator has a significant advantage over others in predicting the outcome of the randomness algorithm.
Simple. This property consists of two parts. First, we want a construction that’s easy to reason about. Second, we don’t want the randomness computation to negatively impact the performance of our consensus algorithm. An ideal randomness generation algorithm should introduce minimal extra communication between validators.

Solorand: Simple Leader-Derived Randomness

The key thing to realize with the strawmans above is that the more choice you give in a randomness scheme, the more likely that scheme is to be gamed. This is because every choice you introduce provides a potential for grinding.

Going with this logic, the following very simple randomness scheme, which we call Solorand, works quite well, and is generally not grindable. As we will discuss, the only downside of this scheme is that it's predictable by the leader, which is undesirable, and which Collaborand fixes.

Define the randomness value computed by Solorand at block N as SOLORAND(N)
Define the designated leader at block N as LEADER(N)
Now, consider the following randomness computation for block N:
- SOLORAND(N) = HASH(SIGNATURE(LEADER(N), SOLORAND(N-1)))

With the above scheme, the randomness at block N is computed from the leader's signature of the randomness at block N-1. Because a signature of a random hash is also a random value, this gives us a way to iterate the randomness within each block in a way that does not require input from anyone. Put another way, using signatures as a source of randomness eliminates choice, which thus helps with grindability.

So, if we go with the above, what are the points of grindability?

The leader can't grind the signature because it is deterministically computed from the previous randomness.
Thus the only thing that a leader can do is choose to omit their value. But doing this would result in the leader timing out, and the next leader being responsible for contributing the signature, thus only affording a validator a single bit of skew each time they're the leader. Moreover, it is important to note that this skew does not compound. The skew introduced by timing out can only impact the randomness in the block directly after the leader, after which all subsequent blocks will be free of any skew due to the fact that a new leader is responsible for computing the randomness for the next block.
But what if the leader has the good fortune of being leader multiple times before the block they want to manipulate? For example, suppose a validator is the leader for M consecutive blocks before the block they want to manipulate. How much skew does the validator get in this case? Perhaps surprisingly, Solarand still only affords this validator one bit of skew for that particular block. How is this the case?

At each block that the leader is responsible for producing, they have two choices: They can either produce the block or timeout. This results in the following set of choices, which collectively provide only a single bit of skew:

Produce all M blocks, including the block they want to manipulate. This is the default scenario in which the leader is acting honestly. This path gives the leader one shot at their event, which has probability p of occurring.
Produce all blocks up to M-1, then let the next validator produce the block they want to manipulate. Because the leader can choose to timeout if they don't like the first option, they can give themselves a second shot at making their event happen, which means they have a second opportunity to hit a second time with probability p.
Timeout somewhere before M-1. But what happens if the leader decides to timeout before M-1? Doesn't that give the leader M-1 more bits of skew? Perhaps surprisingly, it does not if we make the assumption that a leader who times out is not eligible to produce blocks for a little while, as is the case with Revolution and most protocols.The tricky point to understand is that it doesn't matter whether the leader times out right at M-1 or well before M-1. In either case, the randomness is going to be computed by someone other than the leader, which means they can't manipulate it. As such, the leader's only real decision is whether to produce block M with their own randomness, or to allow it to be produced by another validator, which gives them a second shot at hitting their number.

The above means that a malicious actor can only inflate the probability of an event at a particular block very slightly, and only if they have the good fortune of being the leader right before the block whose randomness is being utilized. To be precise, if there is an event with probability p, then the leader can use their single bit of input to grind that probability to 1-(1-p)(1-p) for their block, which is only slightly higher for most values of p. Below are some computed values of the leader's grinded probability, given p, assuming they fully utilize their single bit grindability.
- p = 0.00 -> 0.00
- p = 0.10 -> 0.19
- p = 0.20 -> 0.36
- p = 0.50 -> 0.75
- p = 0.70 -> 0.91
- p = 0.90 -> 0.99

Overall, we think that if the randomness is only being used for something like computing a leader schedule, then Solorand provides a totally workable solution. This is especially true when one considers that PoS schemes are required to make the assumption that no leader controls more than 1/3rd of the stake, which subsequently implies that it is impossible for p to be higher than ~1/3rd.

Collaborand: Consensus-Derived Randomness

While Solorand is perfectly-suitable for use in leader-selection in that it is sufficiently non-grindable and simple, it has the drawback that it is predictable by the leader. In particular, if a leader is lucky enough to be elected for multiple views in a row, then they would know the randomness for all of those blocks ahead of time. Collaborand solves this without re-introducing grindability into our randomness scheme. In particular, Collaborand is able to incorporate randomness from other validators at each block, resulting in a collaborative generation of the randomness that is not grindable, hence the name collaborand.

At a high level, Collaborand selects two contributors to the randomness at each block: The leader and another randomly-chosen validator. The randomness generated by Collaborand is then the combination of signatures from each of these parties.

Concretely, it works as follows:

Define the randomness value computed by Collaborand at block N as COLLABORAND(N)
Define the designated leader at block N as LEADER(N)
Define the randomly-selected validator at block N as RANDOM_VALIDATOR(N), which we will take as being equal to COLLABORAND(N-1) % NUM_VALIDATORS.
Finally, define a signature by a particular validator on a particular payload as SIGNATURE(VALIDATOR, PAYLOAD)
Putting all of the above together, we define the Collaborand randomness as the following (note that || means we concatenate two values):
- COLLABORAND(N) = HASH(SIGNATURE(LEADER(N), COLLABORAND(N-1))||SIGNATURE(RANDOM_VALIDATOR(N-1), COLLABORAND(N-2)))
If the validator's signature is not available, then an empty byte array is used as the second value. We will explain how we can do this without introducing grindability in just a moment.
Additionally, although we opt to use validator N-1's randomness, we can opt to use any previous validator's randomness. As we will see, it may be advantageous to put a few blocks of buffer between the validator's randomness by using N-2 or N-3 instead.

Notably, Collaborand introduces a signature from a random validator at each step in order to make the randomness value unpredictable to both the leader and to all other validators as well. But how does it achieve this without introducing grindability back into the equation? In particular, couldn't the leader simply opt to drop the validator's portion of the randomness opportunistically in order to skew the randomness arbitrarily?

To address this, Collaborand uses a clever scheme for attaching validator randomness that results in the leader being unable to censor the validator randomness as long as at least 1/3rd of validators are honest (the standard assumption in PoS). This scheme works as follows:

Let's assume that we're at block N-1. At this particular block, a random validator designated by RANDOM_VALIDATOR(N-1) is known to everyone on the network to be the supplier of additional randomness.
This validator's job is then to send their randomness value to all other validators on the network. This randomness value is a signature of the prior randomness SIGNATURE(RANDOM_VALIDATOR(N-1), COLLABORAND(N-2)). And note that this broadcast happens the moment that block N-1 is produced.
When a validator goes to vote for block N, it must include in its vote the randomness it received from RANDOM_VALIDATOR(N-1) for the previous block on a best-effort basis.
- Because this randomness is a signature from RANDOM_VALIDATOR(N-1) it can also be verified for authenticity, meaning that nobody can spoof the value generated by this validator, and that all randomness values in the votes for block N must be the same.
Then, when the leader goes to aggregate the votes for block N, they are obligated to use the randomness from RANDOM_VALIDATOR(N-1) that they find in the votes. Note that as long as a single validator has included the proper randomness in their vote, the leader is forced to include the randomness from this validator into their computation for COLLABORAND(N).
- More formally, as long as 1/3rd+1 validators, weighted by stake, submit the value they received for SIGNATURE(RANDOM_VALIDATOR(N-1), COLLABORAND(N-2)) in their vote, the leader is forced to include at least one of the votes from these validators in the next block, or else they will not have the 2/3rds majority needed to propose the block.
If desired, the value of COLLABORAND(N) can opt to use the validator randomness from block N-2 or N-3 instead of the proposed value of N-1. Doing so will just give more time for the randomness to propagate, thus maximizing the likelihood that validators have received and cached the necessary randomness by the time they're ready to vote on block N.

Below is a visual depiction of what Collaborand looks like when executing on Revolution. Notice that we opt to use RANDOM_VALIDATOR(N-2)'s randomness, providing an extra block of buffer time for the randomness to be received by voting validators.

Announcement Phase

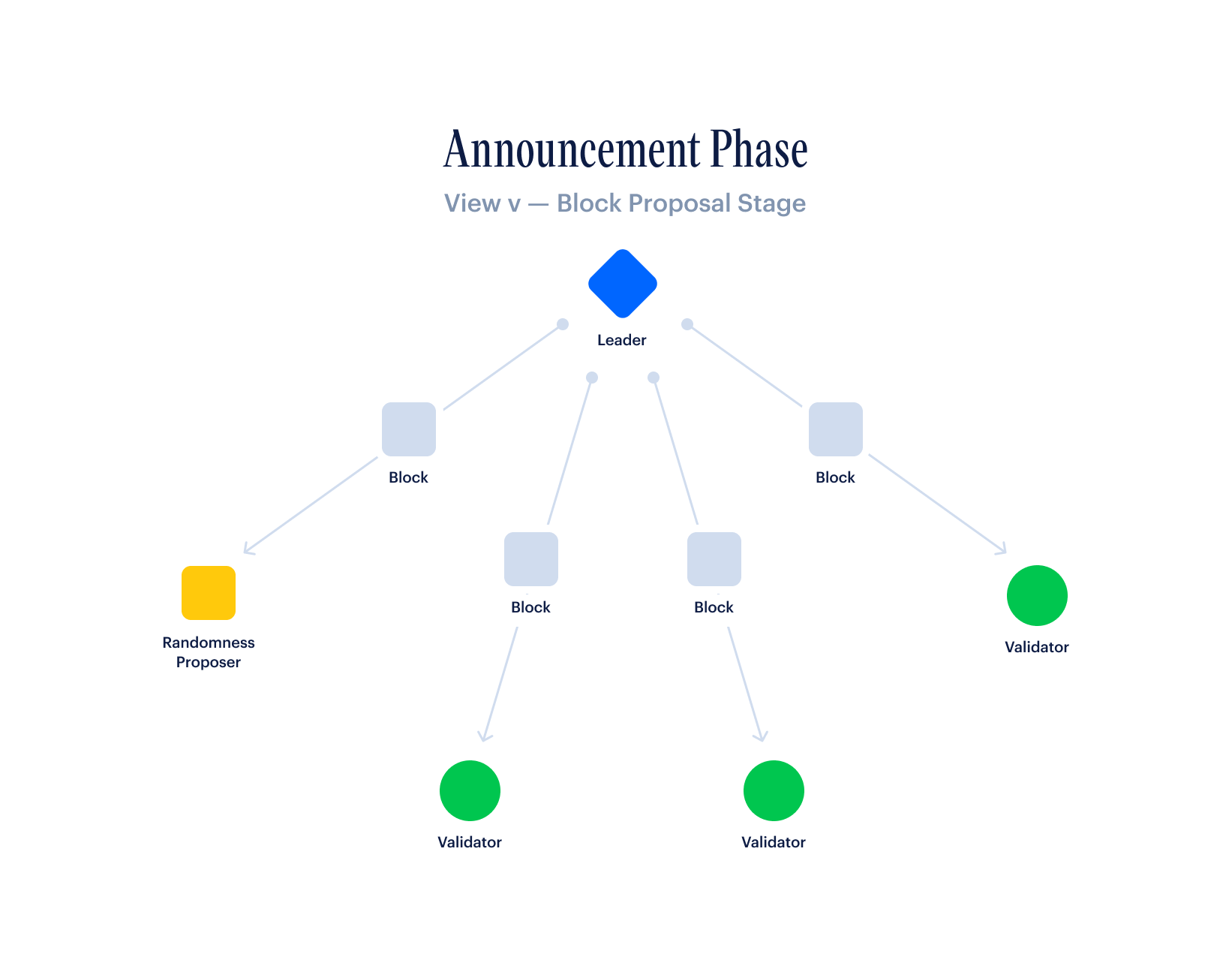
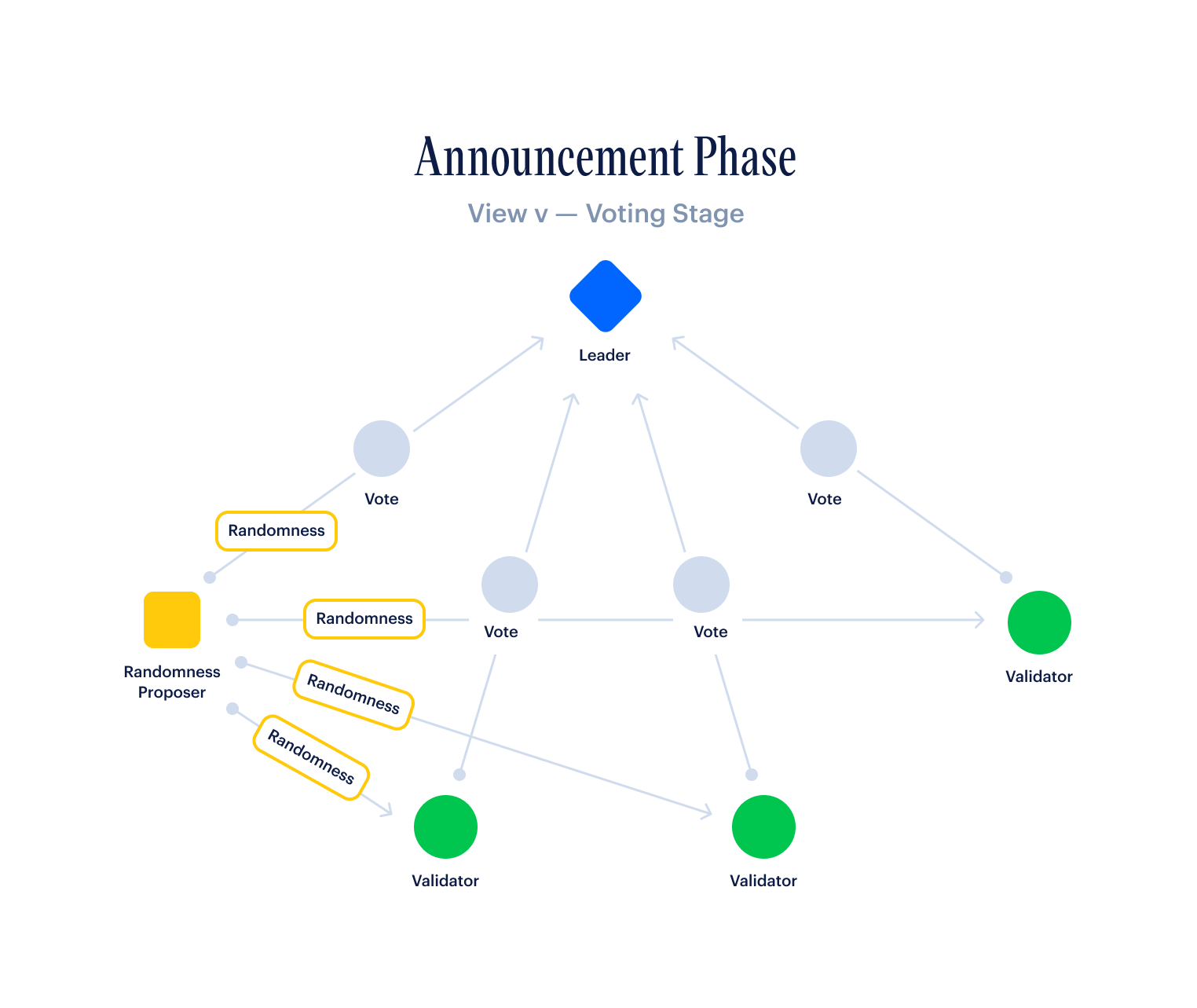
Execution Phase

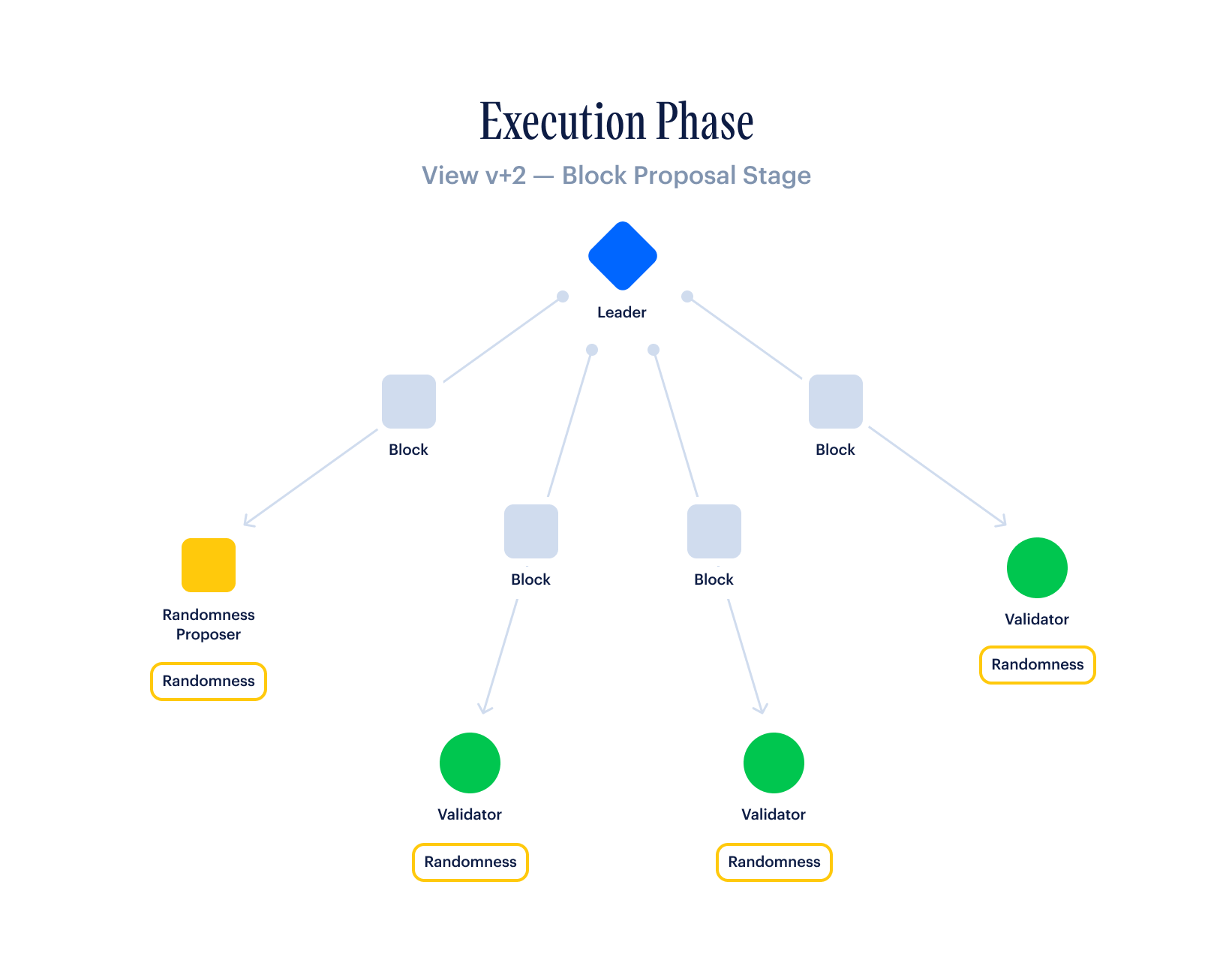
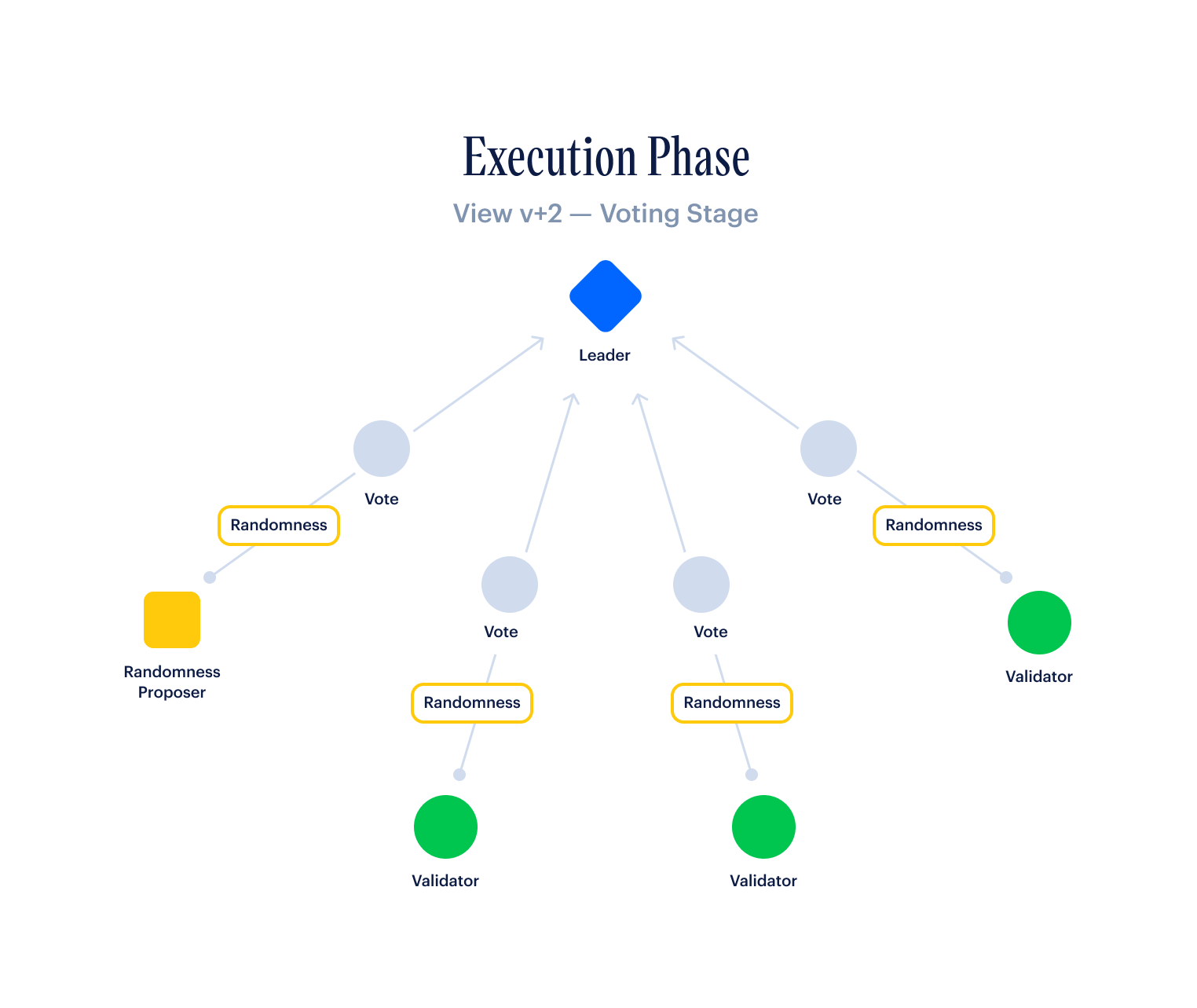
Importantly, the analysis for Collaborand's grindability is virtually identical to that of Solorand's, with the exception that the leader can no longer predict what the randomness value is going to be in the future, even if they are producing many blocks in a row. The leader still maintains one bit of skew for the next block because they can choose to timeout to the next leader. However, note that the validator gets no skew because they cannot predict what value the leader is going to have for their randomness, and therefore get no value out of selectively censoring their contribution.

The Revolution Rule

Most blockchains allow validators to construct blocks however they want, allowing validators the full liberty to reorder transactions however they choose. Bitcoin does this, as does Ethereum and virtually all other PoW and PoS blockchains. But what if, by changing this basic assumption, we could solve the problem of transaction censorship and MEV extraction at the same time?

That is what Revolution achieves with the introduction of a new concept known as the revolution rule, which we will get into in the next section. At a high level, rather than allowing leaders to construct blocks however they want, Revolution requires leaders to follow a particular block construction rule. If a leader constructs a block that does not follow the particular agreed-upon block construction rule, a revolt is triggered by all validators simultaneously, as we will describe, causing the leader to cede their term to the next leader in the Line of Succession.

Put another way, Revolution is able to use information from a validator's mempool, i.e. the transactions that have not yet mined into blocks, in order to detect censorship and timeout the leaders who are causing it.

In what follows, we will describe the concept of revolt in detail, as well as defining a particular block construction rule and revolution rule that result in a peaceful status quo (i.e. one where revolt occurs only if a leader disobeys the block construction rule).

Block Construction and the Revolution Rule

In Revolution PoS, the leader in each view is in charge of constructing the next block, thus choosing which transactions get included and in what order. The rule they use to order the transactions they receive in each block is something we'll refer to as the block construction rule.

When a validator receives a constructed block from their leader, they are then tasked with looking into their mempool to determine whether or not the leader censored any transactions. As one concrete example, a validator may determine that censorship occurred if a high-fee transaction has not been mined for M blocks when it should have been, and automatically timeout the leader if this occurs.

While the above is just one rough example of a rule that a validator could use to timeout a censoring leader, we refer to the general concept of a mempool-defined censorship-detection rule as that validator's revolution rule. In addition, when a validator detects that their revolution rule has been triggered and decides to timeout the current leader as a result, we refer to this timeout as a revolt, mainly to distinguish this type of timeout from a peaceful timeout that occurred for non-censorship reasons.

In practice, while the concept of revolt is useful when discussing the revolution rule, it is important to note that, at the protocol level, there is no need to distinguish between a timeout that occurred as a result of a revolt vs one that occurred for peaceful reasons.

In the next section, we will cover how to design a block construction rule and a revolution rule that are in harmony with one another.

Peaceful Revolution Rules

Unlike other protocols, Revolution requires that the block construction rule not only be agreed-upon by all validators on the network, but that it also be compatible with the revolution rule employed by all validators.

For example, if all validators are running an aggressive revolution rule that revolts on a leader if they don't order transactions strictly by fee, and if a leader is running a block construction rule that frequently puts lower-fee transactions ahead of high-fee transactions (e.g. if they decide to order transactions by when they received them rather than by fee), then this would result in validators frequently revolting on their leaders. When a network's block construction rule is incompatible with its revolution rule in this way, we refer to the revolution rule as a violent revolution rule. This is because violent revolts are bound to occur frequently in such a system.

In contrast, if a revolt can only occur when a leader deviates from the agreed-upon block construction rule, we refer to this as a peaceful revolution rule because revolts will be extremely uncommon. Note that, in order for a revolution rule to be deemed peaceful, it must also be sufficiently-accommodating of network delays, including the reality that transactions may arrive at nodes at significantly different times.

The above definitions yield a very fascinating academic problem: How can we design a block construction rule in combination with a peaceful revolution rule that minimizes both censorship and MEV?

In what follows, we propose what we call a fee-time revolution rule, paired with a fee-time block construction rule. However, it is important to note that much more complex revolution rules can be devised, and we expect this to be an active area of academic research.

Fee-Time Block Construction Rule

Now, to get concrete, we will describe a peaceful revolution rule that complements a block construction rule based on what we refer to as fee-time ordering. We will start by describing the block construction rule that all validators will be expected to follow when constructing blocks, and then we will describe the peaceful revolution rule that goes along with it, which can thwart censorship and MEV extraction.

First, we describe our fee-time block construction rule in detail. Although blocks can technically be constructed in any manner by a leader, following this block construction rule will ensure that leaders are never revolted on by the fee-time revolution rule.

Fee bucketing. First, when a leader receives a transaction, it computes a feePerKilobyte fee rate for it, and puts it in a fee bucket based on this rate. In practice, DeSo nodes running Revolution will have the following fee buckets:
- Bucket #1: 1,000 - 1,500 DESO nanos per kilobyte
- Bucket #2: 1,500 - 2,000 DESO nanos per kilobyte
Time ordering. Within each fee bucket, a leader has the option to order transactions however they want without fear of being revolted on. In practice, we expect most honest leaders will opt to order transactions within a bucket by when they receive them, which is why we refer to this scheme as fee-time ordering. In particular, transactions are first slotted into a fee bucket and then ordered by time of arrival within that bucket.
Block construction. In order to construct a block, a leader is required to include all transactions in the highest fee bucket before including any transactions in a lower fee bucket. As we will see later, this simple rule ensures that users who are paying the highest fees to take an action will never be censored.
Block size. As Revolution produces a block every second, it is natural to include a cap on the number of transactions that can be included in each block. Since DeSo nodes are capable of processing 40,000 transactions per second, and since the typical transaction is 200 bytes, a safe block size would be 8MB. To give nodes some buffer, however, we start with 1MB, or 5,000 transactions per second. Note that the block size is adjustable by the on-chain amendment process, as we will discuss in a later section.
Failing transactions. If a leader encounters a transaction that was initially submitted with a high fee, but that fails when being included in a block, the leader is required to mark this transaction as failing and include it in the block regardless in order to indicate to other validators that they attempted to connect the transaction. In order for a transaction to be marked as failing, the transaction must fail even when processed after all the other transactions in its corresponding fee bucket.
Spam prevention. In the event that a transaction fails to connect when it is time for it to be included in a block, the user who executed the transaction is charged the minimum network fee, which is configured well in advance via the on-chain amendment scheme. Initially, DeSo's minimum fee will be 1,000 DESO nanos per kilobyte, or $0.00001 USD per kilobyte at the current DESO price of ~$10. Transactions that fail are not counted when computing block size, as they will ultimately not be processed.
Mempool balance checking. As part of spam prevention, a validator will accept a transaction into its mempool only if the user who is requesting the transaction has enough to cover the minimum fee for that transaction. This is a very simple check that is quick to perform, and prevents users from being able to overwhelm a node's mempool with invalid transactions.

Fee-Time Revolution Rule

As a complement to the fee-time block construction rule, validators will follow the fee-time revolution rule that we define in this section. This revolution rule ensures that leaders will be revolted on only if they disobey the fee-time block construction rule. This allows validators to quickly timeout leaders who are censoring or attempting to extract MEV by reordering transactions in unfair ways.

Below, we define the fee-time revolution rule in full detail, as well as some accompanying parameters. In what follows, we are describing the process a validator runs after receiving a block from a leader.

Revolt grace period blocks. First, we define a number of blocks that a validator is required to wait after detecting potential censorship before revolting on a leader. This allows our revolution rule to be forgiving in cases where a leader may have simply not received a transaction. The grace period can be relatively short, and DeSo will start with a gracePeriodBlocks of three blocks, or three seconds, since a block is produced every second.
Set a revoltCounter for each transaction. Each transaction in a validator's mempool has a revoltCounter associated with it that is initially zero when it enters the mempool. If the transaction is deemed to be censored in subsequent blocks, its revoltCounter will be incremented. A revolt on the current leader occurs when the revoltCounter exceeds the gracePeriodBlocks.
Find the minFeeRatePerKilobyte of the block. Upon receiving a block, the first thing a validator does is look through the transactions to find the one with the lowest fee per kilobyte. Fees are always referred to using a rate per kilobyte. Once the validator has found the lowest-fee transaction in the block, it saves its fee rate as minFeeRatePerKilobyte.
If the block is not full...
- For excluded transactions, add 1 to their revoltCounter. When a block is not full but the validator has transactions in its mempool that it does not find in the block, this means the leader could be censoring these transactions. As such, the revoltCounter needs to be incremented on each of these transactions.
- Send missing transactions directly to the leader. When transactions are found to be missing from a non-full block, the missing transactions are sent directly to the leader. This gives the leader no excuse for not including them in the very next block.
If the block IS full...
- For each excluded transaction whose fee exceeds minFeeRatePerKilobyte, increment the revoltCounter for that transaction. Whenever a transaction with a high fee is omitted from a full block, while a lower-fee transaction is included, we consider that direct censorship of the transaction, and increment the revoltCounter.
Send missing transactions directly to the leader. This gives the leader no excuse for omitting these transactions from the next block.
If there is a leader change, reset revoltCounter for all transactions. A new leader gets a fresh start.
If any transactions have revoltCounter > gracePeriodBlocks, initiate a revolt. Once a revolt is initiated, this validator will stop voting for blocks produced by the current leader, and instead signal a timeout to the next leader repeatedly, until either:
- Until the current leader is timed out. If the leader is timed out, everything gets reset and we start processing blocks from the new leader.
- Until the current leader produces gracePeriodBlocks with votes from 2/3rds of validators. If we see a number of valid blocks from the leader, with votes from 2/3rds of validators (i.e. with fully-valid Quorum Certificates attached), it means that other validators did not think a revolt was warranted, and so we cancel the coup.

Analyzing the Fee-Time Revolution Rule

The benefit of the fee-time revolution rule is that it is simple to analyze. Pretty much, as long as leaders bucket transactions by fees and don't get too fancy about re-ordering transactions across fee buckets, they will never trigger a validator's revolution rule, and therefore have no chance of ever being revolted on.

In addition, it should be clear that a transaction with a sufficiently high fee cannot be censored for more than gracePeriodBlocks, which DeSo will initially set to three blocks, or three seconds. This means that, as long as at least 1/3rd of validators, weighted by stake, are behaving honestly, a transaction with a sufficiently high fee should generally be expected to move from the mempool into a block within about three seconds at most.

The above is a major improvement over the state of the art, including over Ethereum. In particular, because about 42% of Ethereum validators are censoring TornadoCash transactions, anyone submitting such a transaction must wait an undefined amount of time before a non-censoring validator finally decides to include them in a block. This situation is not only unstable for users, but it is also unfair in the sense that such transactions leave much more time to get front-run by MEV-hunters.

Where the fee-time revolution rule leaves room for improvement is in the amount of fees that it extracts. In particular, while fee-time ordering is simple it is generally likely that breaking fee-time ordering would result in more fees being collected from users. This is because transaction dependencies may make it so that putting a low-fee transaction earlier may result in a high-fee transaction being valid, as opposed to having that transaction become invalid and only pay the minimum fee.

Unfortunately, fully optimizing the fees collected not only requires solving the packing problem, which is known to be NP-hard, but it also becomes a beast of block construction rule, making it extremely difficult for a peaceful revolution rule to be designed and tested. In contrast, fee-time ordering is simple, predictable, and it is easy to show that things work and remain peaceful.

This being said, we certainly don't mean to suggest that a more optimal pair of {block construction rule, revolution rule} does not exist. Quite the contrary. We are excited to see what more efficient rules academics come up with after the concept of revolt has had time to go mainstream.

Magic Nonces

An important implementation detail that comes up when analyzing Ethereum and other PoS protocols is the use of consecutive nonces in transactions, which are used to prevent replay attacks (i.e. processing the same transaction more than once). In particular, because each transaction in Ethereum must include a nonce that is exactly one greater than the nonce in a prior transaction, it leaves no room to reorder transactions within a single user's account. This is actually quite bad from a censorship standpoint because it means that only the first transaction needs to be censored in order for a user's entire transaction chain to disappear.

The reason why Ethereum and other protocols use consecutive nonces like this is because using a random hash, or some other unique identifier to distinguish transactions, requires keeping track of all nonces that have ever been used by a user, rather than just the most recent nonce, as Ethereum does with its scheme.

In contrast, Revolution introduces a new concept we refer to as magic nonces. Rather than requiring nonces to be consecutive, nonces consist of an ExpirationBlockHeight and a PartialID, which can be any valid uint64 value. Simply put, a transaction with a Magic Nonce will be eligible for inclusion in a block as long as its ExpirationBlockHeight is greater than the current block and its PartialID is unique among unexpired transactions. The ExpirationBlockHeight can be at most one day in the future, configurable via an on-chain amendment, and a transaction's PartialID is only stored until it hits its ExpirationBlockHight.

This scheme thwarts replay attacks, just like the consecutive nonce scheme, but it has the major benefit of allowing transactions to be reordered independent of their nonces. This not only enables pure fee-time ordering, but it also increases the amount that validators can make on fees, and makes the user experience much more intuitive for users.

For more information on Magic Nonces, see DeSo's design spec here.

The fee-time revolution rule we've described up until now is what we call an automatic revolution rule, in the sense that it's a rule that all validators can be programmed with, and follow without the need for human intervention.

This being said, there are times where it may be desirable to revolt on a leader for social reasons. For example, suppose a particular leader is producing blocks slowly, but not so slowly as to warrant a timeout. When this behavior is detected at a social level, e.g. by app developers who notice that it's taking a couple extra seconds to finalize transactions, Revolution provides a means of executing a social revolt on such actors.

In particular, every validator will have an admin panel through which they can specify peer validators on which they'd like to run a social revolt. When a peer is manually added to this list, the validator will still accept blocks produced by the peer, but they will never vote on blocks produced by them. Instead, they will signal a timeout, thus making it harder for that peer to get the 2/3rds majority it needs for its blocks. If at least 1/3rds of all validators by stake do this to a particular validator, that validator will be effectively blacklisted from producing blocks, always automatically timing out to the next leader in the Line of Succession.

This mechanic can be used to thwart many nefarious validator behaviors, not just slowness. For example, if a particular validator begins to accumulate a concentration of stake that is uncomfortably high, a social revolt can begin, thus strongly incentivizing stakers to move away from that validator.

The Burn-Maximizing Fee Algorithm (The BMF)

Revolution introduces a network fee model which benefits the constituents of the network as well as their coin holdings during periods of high transaction demand known as the Burn-Maximizing Fee (BMF) model. In existing proof-of-stake networks, periods of unusually high network congestion result in network validators collecting a disproportionate share of user fees for no additional work. This is because users are left bidding for the limited throughput capacity of the network, and these bids are collected by network validators.

However, network throughput capacity doesn't fluctuate in response to users and their bids for block space. The network's throughput capacity is fixed whether users are willing to bid $1 per transaction or $1,000 per transaction. This mismatch between the social cost of committing a transaction (how much users are willing to pay) and the operational cost of committing a transaction (how much validators pay in infrastructure expenses) leads to socially unproductive and perverse incentives for validators during periods of high transaction demand.

To benefit the network’s users rather than the network’s validators the BMF extends Ethereum’s EIP-1159 fee model to maximally burn away the difference between the social and operational costs of a transaction.

The BMF at a high level works as follows:

A moving average of the fees paid by users is computed over the most recent N blocks.
1. For DeSo, N will be 3600 blocks, adjustable by an on-chain amendment. Also notice there are other parameters that need to be considered here, like the soft block limit and the hard block limit, which we ignore for now.
Similar to EIP-1159: We compute this moving average and denote it the minFee for the network.
Unlike EIP-1159: The reward collected by a validator for committing a subsequent transaction is:
1. max(log_2(txnFee - minFee), 0)
2. Note that a base unit is the smallest unit of currency that a protocol allows (like a satoshi in Bitcoin). For DeSo, the base unit is a nano (noting that 1,000,000,000 nanos = 1 DESO).

Compared to Ethereum’s EIP-1159, the BMF is extremely efficient at dealing with periods of high transaction demand, and benefiting the network’s constituents as a result. The BMF uses a logarithmic function to maximally burn transaction fees across the network, making the protocol strongly deflationary as a result. To give an example on why the BMF is so powerful, consider the situation below:

An extremely sought after NFT collection is to go up for sale at midnight. The preceding day had low transaction throughput across the network – dropping the minFee to near-zero as a result. The second the NFT collection goes up for sale, network users create transactions paying $1,000s in fees in an attempt to get the NFTs first.
In the naive fee model utilized by most chains: These $1,000s in fees are pocketed by the lucky validator who gets to produce the block containing their bids. The validator has made a killing without providing any additional services for the network. Worse yet, the large fees incentivize validators to fight at a consensus level to be the validator who commits the block.
In the EIP-1159 fee model utilized by Ethereum: The $1,000s in fees are still pocketed by the lucky validator, as the minFee running average was set to ~$0 for the preceding day. Worse, Ethereum’s protocol provides a clear mapping as to what validator will be responsible for network transactions submitted at midnight. This creates toxic incentives for how users, validators, and NFT creators might collude in an effort to collect transaction fees. For example, an NFT creator may time the release of their collection to correspond with when their friend is the network’s validator responsible for processing transactions. These socially unproductive fee models continually harm the network, its users, and its applications.
In the BMF fee model used by Revolution: Validators are still incentivized to include the transactions paying the highest fees given the monotonically increasing nature of the logarithm function.

However, even if the validator included transactions paying $1,000,000 in total fees, the validator takes as reward only log_2($1,000,000) = $20 in fees. The remaining $999,980 is burned making periods of high throughput extremely deflationary for the network and its users.

These extremely deflationary measures make Revolution’s fee model benefit its users rather than its validators. In addition, it provides little incentive for validators to collude in an effort to collect transaction fees, unlike all aforementioned fee models.

Given all of the above, we believe the BMF will make Revolution the first network where coin holders and users are protected from centralized profiteering during periods of high transactional volatility.

Dynamic Block Rewards

In what follows, we use DESO to refer to the base currency of the blockchain implementing Revolution. We do this as a convenience, as the DeSo blockchain is the first blockchain that will be implementing Revolution PoS. If you want to use Revolution for your own distinct blockchain, simply replace all references to DESO with your blockchain's native currency.

Revolution uses block rewards as an incentive system for network participants to propose, validate, and vote on blocks. By ensuring the liveness and security of the network, validators can receive block rewards as payment from the protocol every time they finalize a block. A successful reward system must have two properties:

A significant percentage of DESO is staked to secure the network, ensuring that a minority of stake cannot subvert the protocol
Validators are incentivized to remain online to propose, validate, and vote on blocks, ensuring the liveness of the network

Total Network Stake & Block Reward Amount

To ensure a significant enough amount of DESO is staked to secure the network, the protocol automatically adjusts the block rewards to incentivize network participants to stake more or less DESO.

Block rewards adjust dynamically as a function of the total amount of DESO staked. If too little DESO is staked in the network, the protocol automatically increases the block rewards, which incentivizes network participants to stake more DESO.

However, past a certain threshold of total DESO staked by the network, any additional stake in the network yields diminishing returns in securing the network. So, if more DESO is staked beyond the network’s target range, the protocol automatically decreases the block rewards to ensure that it is not overcompensating validators for providing little additional security for the network.

We call this self-adjusting reward mechanism a Dynamic Block Reward. The mechanism has four configuration parameters, all of which can be updated by on-chain amendments:

A target window for the total amount of DESO that needs to be staked to secure the network. The window has two components:
- A constant lower bound for the target DESO amount to be staked
- A constant upper bound for the target DESO amount to be staked
A constant epoch duration, defined as a number of blocks. The block reward for an epoch is computed at the end of the previous epoch and does not change during an epoch
A constant block reward delta, used to increase or decrease the block reward

At the end of each epoch, the protocol uses a simple algorithm to determine the block reward for the next epoch. It compares a snapshot of the total network stake with the configured target window. There are three possibilities:

If the total network stake is within the target window, the block reward for the next epoch remains the same.
If the total network stake is greater than the upper bound of the target window, the block reward for the next epoch is reduced by the block reward delta. This incentivizes network participants to reduce their stake, as they will earn lower rewards moving forward.
If the total network stake is less than the lower bound of the target window, the block reward for the next epoch is increased by the block reward delta. This incentivizes network participants to increase their stake and earn more rewards.

Incentivized Behavior for Validators & Leaders

We need to incentivize validators to remain online, validate blocks, and vote on as many blocks as possible. We additionally want to incentivize leaders to remain online, and propose blocks with minimal latency, while including votes from as many validators as feasible.

The protocol implements a unique scheme for distributing block rewards amongst validators and leaders when they behave as desired. Notably, it does not slash validators’ stakes. Our expectation is that the opportunity cost of missed block rewards simplifies the protocol meaningfully and provides the proper incentives for the desired behavior from network participants, without need for slashing.

Block Reward Algorithm

In Fast HotStuff, every block contains a QC made up of the list of validators votes for the previous block. Every block has one block reward transaction that pays out a reward to one leader and validator who have successfully proposed and voted on a block at some point in the past.

Each time a leader finalizes a block b_n with QC_n and can propose a new block b_n+2, it uses the following algorithm to determine the block reward for block b_n+2:

It builds a stake-ordered list V_n of size |V_n| made up of all of the validators that were registered when block b_n was committed. V_n includes all validators whether or not their vote was included in QC_n
It computes a random index i where 0 <= i < |V_n| that will be used to select a random validator from V. The formula to compute the index i looks as follows:

i = COLLABORAND(N) % |V_n|

The randomly selected validator V_n(i) is eligible to receive the block reward for b_n+2 if they are in the QC for block b_n

If V_n(i) has not had their vote included in the QC_n, then there will be no block reward included in b_n+2. However, if V(i) had their vote included in the QC_n, then:

V_n(i) gets the block reward for in b_n+2 for their past vote in b_n
The leader L_n who proposed block b_n gets a percentage of the block reward for successfully proposing b_n and including V_n(i)’s vote in QC_n

This scheme results in a two-block lagging payment schedule for block rewards. L_n successfully proposes b_n and includes a vote from V_n(i) in QC_n. Both only get rewarded for their efforts two blocks later in b_n+2.

Notably, each block can result in at most one validator and one leader receiving the block reward. It is entirely possible for a block to not include a reward if the selected validator for that block has not voted in the past.

Advantages

This approach diverges from other blockchains’ approaches for validator rewards in that it results in at most one validator and leader who are eligible to receive the block reward. The approach has a number of advantages:

The algorithm to select the validator eligible to receive the reward for each block is a constant time operation that is efficient to compute. In practice, the two-block lagging payment schedule ends up being quite short (< 10 seconds) and results in minimal delay for rewards.
Validators are incentivized to vote on every block, to increase the number of blocks they are eligible to receive rewards for. Over a long period of time, each validator is paid out rewards in proportion with their relative stake to the rest of the network.
Leaders are financially incentivized to include as many votes as possible in each QC, to increase their chances of receiving a kickback for including the selected validators’ vote for a block reward. In a repeated game, where the same node is the leader for an extended period of time, this becomes game theory optimal behavior for leaders.

Risks

This approach does have one inherent risk in its incentive for validators. Validators are incentivized to vote as quickly as possible on each block to increase their vote’s likelihood of being included in a QC. However, this means that there is no mechanism to enforce that validators actually validate every block before broadcasting their vote. Given the expectation that the set of validators with ⅔ of the total stake are honest, we do not believe this is significant enough to warrant an additional enforcement mechanism. Rather, validators have a financial interest in maintaining the long-term integrity of the network. Voting for and committing invalid blocks is a significant and easily detectable threat that undermines this.

Rewards for Stake Delegation

The Dynamic Block Reward pays out block rewards directly to validators and leaders. While the protocol’s staking delegation mechanism allows regular users to delegate their stake to validators nodes, it does not provide a built-in mechanism to pay out rewards directly to stake delegators. Rather, it leaves room for validators and stake delegators to separately decide on the reward share for stake delegators.

By not prescribing a standard mechanism for splitting block rewards between validators and stake delegators, we leave room for a market to form around staking services. Each validator that intends to accept delegated stake from users can offer its own incentive structure and unique value-add features. In the long run, we expect this to form a market for stake delegation that is feature rich and decoupled from the core mechanism for Dynamic Block Rewards.

On-Chain Amendments

Every Proof of Stake protocol has tunable global parameters that all validators need to agree on, which greatly impact the functioning of the network. These values include critical economic parameters like how much will be paid in block rewards and what yields should be set to, but they also include more mundane things like how long validators should wait before timing out a leader.

In all other protocols we've reviewed, including major protocols like Ethereum, global parameters are adjusted by an oligarchy of developers who control the core code repository, with limited input from token-holders. This centralized process not only results in politics forming around the core developers, but it also ultimately does a very poor job of taking into account the interests of token-holders, i.e. the will of the people.

With Revolution, we introduce a new mechanism for updating these parameters that is by the token-holders, for the token-holders called on-chain amendments. On-chain amendments make it so that all critical network parameters are updated via a manual validator vote that happens on-chain with full transparency. Every validator gets to vote on network parameter changes with a weight that is proportional to their stake. This makes on-chain amendments a 1:1 reflection of token-holder interests, i.e. the will of the people.

To maximize decentralization, proposals for on-chain amendment votes can be submitted by anyone who has an amount of stake exceeding a threshold. This threshold is itself a parameter that can be updated by an on-chain amendment.

On-chain amendment proposals will include some expiration period (above a minimum threshold) in which validators will be required to respond. To encourage participation, failure to submit a vote in time will result in a validator being ineligible for block rewards for some number of blocks.

Upon a proposal's expiration, if enough votes have been cast (as weighted by stake), the leading vote (as weighted by stake) may result in an update of the global parameters set within the protocol. With this mechanism for parameter updating via transparent on-chain voting, we hope to establish a self-governing consensus protocol that is run by the token-holders, for the token-holders.

Applicable Parameters

Whenever an on-chain amendment proposal is submitted, it will include a set of parameters that the proposer wishes to change. Below is a preview of some of the parameters that will be adjustable via on-chain amendments, some of which were mentioned in this document.

Staking

Cooldown period between a validator registering and being able to unregister (initially 3 epochs, ~3 hours)
Lockup period between a user unstaking and being able to unlock their stake (initially 3 epochs, ~3 hours)

Leader Schedule

Leader schedule epoch length (initially 3,600 blocks, ~1 hour)
First timeout length (initially 30 seconds)
Minimum stake required for a validator to be eligible to vote on blocks (initially 100 DESO)
Minimum stake required for a validator to be eligible to become a leader (initially 100 DESO)
Maximum number of validators eligible to be included in a leader schedule (initially unlimited)

Dynamic Block Rewards

Lower bound target for the amount of DESO staked on the network (initially 10%)
Upper bound target for the amount of DESO staked on the network (initially 25%)
Block reward epoch length (initially 3,600 blocks, ~1 hour)
Block reward delta used to increase or decrease the block reward each epoch when target stake or number of validators are outside of their desired ranges (initially 0.05% per hour, or ~9% per week)
Block reward percentage paid to the leader (initially 5%)
- Whatever does not go to the leader is paid to a randomly-selected validator on each block.

Burn-Maximizing Fees

Number of recent blocks over which to calculate the average fee paid by users (initially 3,600 blocks, ~1 hour)
Minimum number of recent blocks used to calculate average fee paid (initially 300 blocks, ~5 mins)
Maximum number of recent blocks used to calculate average fee paid (initially 86,400 blocks, ~1 day)

Revolution

Duration of observed transaction censorship before triggering a revolution timeout vote (initially 3 blocks, ~3 seconds)
Fee-time bucket size (initially 500 DESO nanos, e.g. buckets of 1000-1500 DESO nanos, 1500-2000 DESO nanos, etc.)
Maximum block size (initially 8mb)
Minimum network fee (initially 1,000 DESO nanos per kb, or ~$0.00001 USD per kilobyte at the current DESO price of ~$10)
Max nonce expiration window (initially 86,400 blocks, ~1 day into the future)

On-Chain Amendment Parameters

Minimum stake required for a validator to be eligible to propose on-chain amendments for global parameter updates (initially ?)
Minimum stake required for a validator to be eligible to vote in on-chain amendments for global parameter updates (initially 100 DESO)
Minimum poll length (initially 86,400 blocks, ~1 day)
Block rewards ineligibility period if a validator fails to vote on an on-chain amendment proposal (initially ~1 week’s worth of blocks)
Minimum percent of total stake required for an on-chain amendment poll to pass and finalize upon expiration (initially 10% of stake)

Liquid Bonding

As Revolution is technically a complete and secure protocol without Liquid Bonding, and since Liquid Bonding is a significant innovation on its own, we have decided to break the introduction of Liquid Bonding into its own document.

If you would like early access to our Liquid Bonding proposal, contact one of the authors listed at the top of this paper.

Conclusion

Although Bitcoin has been around since 2008, and although our team has been researching consensus protocols for over a decade, our honest assessment before we developed Revolution was that no protocol had really matched Bitcoin's Proof of Work in terms of its potential for decentralization, its censorship-resistance, its permission-lessness, and its simplicity. That last part, simplicity, is especially important to us because we don't think Bitcoin would have become as big as it has today without Satoshi's ability to boil the protocol down into something that anyone with a basic understanding of Computer Science could fully grasp.

For that reason, we take immense pride in Revolution as a protocol that not only achieves comparable levels of decentralization, censorship-resistance, and permissionless-ness to Bitcoin but that also maintains a level of simplicity that fosters accessibility and understanding. We cautiously hope that, in time, Revolution will be able to do for Proof of Stake what Bitcoin did for Proof of Work — establishing a new benchmark for Proof of Stake designs and inspiring further innovation in decentralized systems.

Abstract​

Introduction​

Background on Proof of Stake Mechanisms​

Starting with Proof of Work​

From Proof of Work to Proof of Stake (Tendermint)​

Faulty Leaders and Timeouts​

From Tendermint to HotStuff​

O(n2) -> O(n) Communication Overhead​

Block Pipelining​

Reducing One More Round with Fast HotStuff​

Revolution Proof of Stake​

The Lifecycle of a Node​

Netboot: Censorship-Resistant DNS Bootstrapping​

HyperSync: Efficient Snapshot Bootstrapping​

Elliptic Sum​

Ancestral Records​

Putting it All Together​

Sovereign Staking (a.k.a. No-Lockup Staking)​

Registering as a Validator​

Staking​

Block Rewards​

Unstaking​

Validator Hub​

Fast HotStuff In-Depth​

The Gist of Fast HotStuff​

Fast HotStuff Pseudocode​

A Note on BLS Signatures​

Line of Succession Leader Scheduling​

Election and Line of Succession​

Mechanics of The Election​

Performance Advantages​

Network Configuration​

Eligibility for Leadership​

Epoch Duration​

Timeouts and Timeout Duration Exponential Backoff​

Solorand & Collaborand - Robust On-Chain Randomness​

Why On-Chain Randomness is Hard​

Desirable Properties​

Solorand: Simple Leader-Derived Randomness​

Collaborand: Consensus-Derived Randomness​

Announcement Phase​

Execution Phase​

The Revolution Rule​

Block Construction and the Revolution Rule​

Peaceful Revolution Rules​

Fee-Time Block Construction Rule​

Fee-Time Revolution Rule​

Analyzing the Fee-Time Revolution Rule​

Magic Nonces​

Social Revolution​

The Burn-Maximizing Fee Algorithm (The BMF)​

Dynamic Block Rewards​

Total Network Stake & Block Reward Amount​

Incentivized Behavior for Validators & Leaders​

Block Reward Algorithm​

Advantages​

Risks​

Rewards for Stake Delegation​

On-Chain Amendments​

Applicable Parameters​

Staking​

Leader Schedule​

Dynamic Block Rewards​

Burn-Maximizing Fees​

Revolution​

On-Chain Amendment Parameters​

Liquid Bonding​

Conclusion​

Abstract

Introduction

Background on Proof of Stake Mechanisms

Starting with Proof of Work

From Proof of Work to Proof of Stake (Tendermint)

Faulty Leaders and Timeouts

From Tendermint to HotStuff

O(n²) -> O(n) Communication Overhead

Block Pipelining

Reducing One More Round with Fast HotStuff

Revolution Proof of Stake

The Lifecycle of a Node

Netboot: Censorship-Resistant DNS Bootstrapping

HyperSync: Efficient Snapshot Bootstrapping

Elliptic Sum

Ancestral Records

Putting it All Together

Sovereign Staking (a.k.a. No-Lockup Staking)

Registering as a Validator

Staking

Block Rewards

Unstaking

Validator Hub

Fast HotStuff In-Depth

The Gist of Fast HotStuff

Fast HotStuff Pseudocode

A Note on BLS Signatures

Line of Succession Leader Scheduling

Election and Line of Succession

Mechanics of The Election

Performance Advantages

Network Configuration

Eligibility for Leadership

Epoch Duration

Timeouts and Timeout Duration Exponential Backoff

Solorand & Collaborand - Robust On-Chain Randomness

Why On-Chain Randomness is Hard

Desirable Properties

Solorand: Simple Leader-Derived Randomness

Collaborand: Consensus-Derived Randomness

Announcement Phase

Execution Phase

The Revolution Rule

Block Construction and the Revolution Rule

Peaceful Revolution Rules

Fee-Time Block Construction Rule

Fee-Time Revolution Rule

Analyzing the Fee-Time Revolution Rule

Magic Nonces

Social Revolution

The Burn-Maximizing Fee Algorithm (The BMF)

Dynamic Block Rewards

Total Network Stake & Block Reward Amount

Incentivized Behavior for Validators & Leaders

Block Reward Algorithm

Advantages

Risks

Rewards for Stake Delegation

On-Chain Amendments

Applicable Parameters

Staking

Leader Schedule

Dynamic Block Rewards

Burn-Maximizing Fees

Revolution

On-Chain Amendment Parameters

Liquid Bonding

Conclusion